Question

If

$\tan \theta + \tan 2\theta + \tan 3\theta = \tan \theta \tan 2\theta \tan 3\theta$

then the general value of $\theta$ is

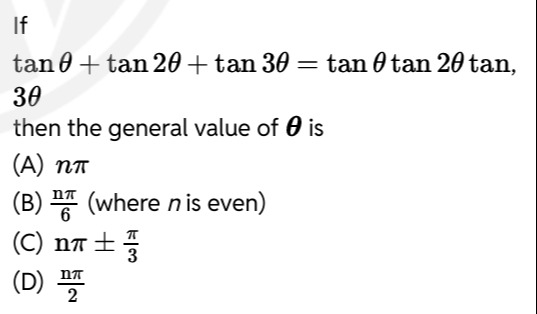
• A. n\pi
• B. \frac{n\pi}{6} (where n is even)
• C. n\pi \pm \frac{\pi}{3}
• D. \frac{n\pi}{2}

Answer 1

Answer: (B)

\frac{n\pi}{6} (where n is even)

Answer 2

The given equation is $\tan \theta + \tan 2\theta + \tan 3\theta = \tan \theta \tan 2\theta \tan 3\theta$. This equation is of the form $\tan A + \tan B + \tan C = \tan A \tan B \tan C$, where $A=\theta$, $B=2\theta$, and $C=3\theta$. This identity holds if $A+B+C = n\pi$ for some integer $n$, provided that $\tan A, \tan B, \tan C$ are defined. So, $\theta + 2\theta + 3\theta = n\pi$, which simplifies to $6\theta = n\pi$. Thus, $\theta = \frac{n\pi}{6}$.

We need to ensure that $\tan\theta$, $\tan 2\theta$, and $\tan 3\theta$ are defined. $\tan x$ is undefined when $x = k\pi + \frac{\pi}{2}$ for some integer $k$.

1. $\tan\theta$ is undefined if $\theta = k\pi + \frac{\pi}{2}$. $\frac{n\pi}{6} = k\pi + \frac{\pi}{2} \implies n = 6k + 3$. This means $n$ must be odd.

2. $\tan 2\theta$ is undefined if $2\theta = k\pi + \frac{\pi}{2}$. $2\left(\frac{n\pi}{6}\right) = k\pi + \frac{\pi}{2} \implies \frac{n\pi}{3} = k\pi + \frac{\pi}{2} \implies n = 3k + \frac{3}{2}$. This is not possible for integer $n$.

3. $\tan 3\theta$ is undefined if $3\theta = k\pi + \frac{\pi}{2}$. $3\left(\frac{n\pi}{6}\right) = k\pi + \frac{\pi}{2} \implies \frac{n\pi}{2} = k\pi + \frac{\pi}{2} \implies n = 2k + 1$. This means $n$ must be odd.

For $\theta = \frac{n\pi}{6}$ to be a valid solution, $n$ must not be odd. Therefore, $n$ must be an even integer. Let $n = 2m$ for some integer $m$. Then $\theta = \frac{2m\pi}{6} = \frac{m\pi}{3}$. This corresponds to the option $\frac{n\pi}{6}$ where $n$ is even.