Question

If $\tan \,\theta = - 2$ and $\theta$ lies in the second quadrant. find the values of other trigonometric functions.

Answer 1

Hint : Here one trigonometric ratio is given. In this question we have to find the values of the other trigonometric functions. By using the Pythagoras theorem and the definition of trigonometric ratios we determine the solution for the given question.

Complete step by step solution:
The question is related to trigonometry and it includes the trigonometry ratios. The trigonometry ratios are sine, cosine, tangent, cosecant, secant and cotangent. In trigonometry the cosecant trigonometry ratio is the reciprocal to the sine trigonometry ratio. The secant trigonometry ratio is the reciprocal to the cosine trigonometry ratio and the cotangent trigonometry ratio is the reciprocal to the tangent trigonometry ratio.
The tangent trigonometry ratio is defined as $\tan x = \dfrac{{\sin x}}{{\cos x}}$ , The cosecant trigonometry ratio is defined as $\csc x = \dfrac{1}{{\sin x}}$ , The secant trigonometry ratio is defined as $\sec x = \dfrac{1}{{\cos x}}$ and The tangent trigonometry ratio is defined as $\cot x = \dfrac{{\cos x}}{{\sin x}}$
The trigonometric ratios are written by considering the right-angled triangle.

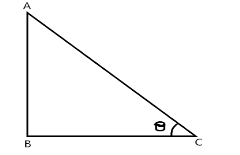
The tangent trigonometric ratio is defined according to the right-angled triangle is
$\tan \,\theta = \dfrac{{opposite}}{{adjacent}}$
Therefore, the trigonometric ratio is written as
$\Rightarrow \tan \,\theta = - 2$
Here the opposite side of the angle $\theta$ is AB and the adjacent side of the angle $\theta$ is BC. The AB is a positive and the BC is a negative because it lies in the second quadrant.
It is written as
$\Rightarrow \tan \,\theta = \dfrac{2}{{ - 1}}$
Here the value of AB is 2 and the value of BC is -1. We can determine the value of AC by using the Pythagoras theorem. The Pythagoras theorem is stated as that the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. i.e., $A{B^2} + B{C^2} = A{C^2}$
Therefore we have
$\Rightarrow {2^2} + {( - 1)^2} = A{C^2}$
On simplifying it is written as
$\Rightarrow 4 + 1 = A{C^2}$
$\Rightarrow A{C^2} = 5$
Taking square root on both sides we get
$\Rightarrow AC = \sqrt 5$
The value will be positive
The sine trigonometry ratio is defined as
$\sin \,\theta = \dfrac{{opposite}}{{hypotenuse}} = \dfrac{{AB}}{{AC}}$
Therefore by substituting the values we get
$\sin \,\theta = \dfrac{{AB}}{{AC}} = \dfrac{2}{{\sqrt 5 }}$
The cosine trigonometry ratio is defined as
$\cos \,\theta = \dfrac{{adjacent}}{{hypotenuse}} = \dfrac{{BC}}{{AC}}$
Therefore by substituting the values we get
$\cos \,\theta = \dfrac{{BC}}{{AC}} = \dfrac{{ - 1}}{{\sqrt 5 }}$
The cosecant trigonometry ratio is defined as
$\csc \,\theta = \dfrac{1}{{\sin \,\theta }}$
Therefore by substituting the values we get
$\csc \,\theta = \dfrac{{\sqrt 5 }}{2}$
The secant trigonometry ratio is defined as
$\sec \,\theta = \dfrac{1}{{\cos \,\theta }}$
Therefore by substituting the values we get
$\sec \,\theta = - \sqrt 5$
The cotangent trigonometry ratio is defined as
$\cot \,\theta = \dfrac{1}{{\tan \,\theta }}$
Therefore by substituting the values we get
$\cot \,\theta = \dfrac{{ - 1}}{2}$
Hence we have determined the all trigonometric ratios.

Note : In the trigonometry we have six trigonometry ratios and 3 trigonometry standard identities. The trigonometry ratios are sine, cosine, tangent, cosecant, secant and cotangent. These are abbreviated as sin, cos, tan, cosec or csc, sec and cot. The above question is also solved by using the standard trigonometry formulas on sine and cosine.