Question

If $\tan {\theta _1}.\tan {\theta _2} = - \dfrac{{{a^2}}}{{{b^2}}}$ then the chord joining two points ${\theta _1}$ & ${\theta _2}$ on the ellipse $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$ will subtend a right angle at:
A. Focus
B. Centre
C. End of the major axis
D. End of the minor axis

Answer 1

An ellipse can be defined as the locus of all points that satisfy the equations: $x = a\cos \theta$ and $y = b\sin \theta$ . So, any point on the ellipse is of the form $x = a\cos \theta$ and $y = b\sin \theta$ . Using this, we can find two points given in question and also find their slope.

Complete step-by-step answer:
In the question, the ellipse is given with the equation $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$ with origin at point $O(0,0)$ .

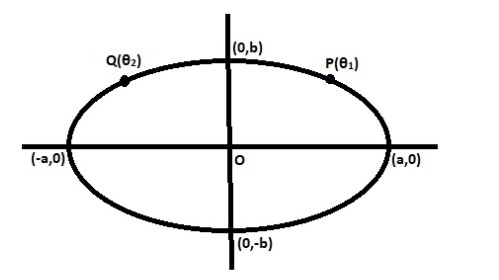
Let us take two points $P({\theta _1})$ and $Q({\theta _2})$ as shown in the figure.
Now, as we know that an ellipse can be defined as the locus of all points that satisfy the equations: $x = a\cos \theta$ and $y = b\sin \theta$ .
Therefore, according to the definition stated above,
Point $P({\theta _1}) = (a\cos {\theta _1},b\sin {\theta _1})$
Point $Q({\theta _2}) = (a\cos {\theta _2},b\sin {\theta _2})$
Now, to find the slope $m$ of points $({x_1},{y_1})$ and $({x_2},{y_2})$ , we can use the following formula: $m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$
Therefore, slope of line $OP = m(OP) = \dfrac{{b\sin {\theta _1} - 0}}{{a\cos {\theta _1} - 0}} = \dfrac{b}{a}\tan {\theta _1}$
Slope of line $OQ = m(OQ) = \dfrac{{b\sin {\theta _2} - 0}}{{a\cos {\theta _2} - 0}} = \dfrac{b}{a}\tan {\theta _2}$
Now, multiplying and $m(OQ)$ as we are given that $\tan {\theta _1}.\tan {\theta _2} = - \dfrac{{{a^2}}}{{{b^2}}}$ , we get
$m(OP) \times m(OQ) = \dfrac{b}{a}\tan {\theta _1} \times \dfrac{b}{a}\tan {\theta _2} = \dfrac{{{b^2}}}{{{a^2}}}\tan {\theta _1}\tan {\theta _2} = \dfrac{{{b^2}}}{{{a^2}}} \times - \dfrac{{{a^2}}}{{{b^2}}}$
Or, $m(OP) \times m(OQ) = - 1$
Since, the product of slope comes out to be $- 1$, so it represents a perpendicular pair of straight lines.
Therefore, chord PQ subtends the right angle at the centre of the ellipse.
Therefore, Centre is the required answer.

So, the correct answer is “Option B”.

Note: The two points can be taken in any of the quadrants in general, as it does not matter because the angle will be different and will make up for it. The important thing to remember is that any point on the ellipse should be known in parametric form to solve such types of questions.