Question

If $\tan \left( {{\sec }^{-1}}x \right)=\sin \left( {{\cos }^{-1}}\dfrac{1}{\sqrt{5}} \right)$ , then $x=$
A.$\pm \dfrac{3}{\sqrt{5}}$
B.$\pm \dfrac{\sqrt{5}}{3}$
C.$\pm \dfrac{\sqrt{3}}{5}$
D.None of these

Answer 1

Hint: Express ${{\sec }^{-1}}x$ inside tan function to ${{\tan }^{-1}}$ by making a right angles triangle using $\sec \theta =\left( \dfrac{\text{Hypotenuse}}{\text{Base}} \right)$ . Use Pythagoras theorem ${{\left( \text{Hypotenuse} \right)}^{2}}={{\left( \text{Base} \right)}^{2}}+{{\left( \text{Perpendicular} \right)}^{2}}$ to get the other side of triangle. Now, express ${{\sec }^{-1}}$ to ${{\tan }^{-1}}$ using $\tan \theta =\dfrac{\text{Perpendicular}}{\text{Base}}$ . Similarly, make a triangle using ${{\cos }^{-1}}\dfrac{1}{\sqrt{5}}$ for R.H.S by following result:
$\cos \theta =\dfrac{Base}{Hypotenuse}$
Use Pythagoras theorem to get the other side of this triangle as well. Now, convert ${{\cos }^{-1}}$ to ${{\sin }^{-1}}$ function using $\sin \theta =\dfrac{\text{Perpendicular}}{\text{Hypotenuse}}$
Use the following results: $\tan \left( {{\tan }^{-1}}\theta \right)=\theta$ and $\sin \left( {{\sin }^{-1}}\theta \right)=\theta$

Here, we have to determine value of x, if $\tan \left( {{\sec }^{-1}}x \right)=\sin \left( {{\cos }^{-1}}\dfrac{1}{\sqrt{5}} \right)$ ……………………(i)

Complete step-by-step answer:
So, let us simplify LHS and RHS of the above equation individually. So, LHS of the equation (i) is given as
$\Rightarrow LHS=\tan \left( {{\sec }^{-1}}x \right)$ ………………………………………(ii)
Now, as we know the trigonometric relation for $\sec \theta$ is given as
$\Rightarrow \sec \theta =\left( \dfrac{\text{Hypotenuse}}{\text{Base}} \right)$
$\Rightarrow \theta ={{\sec }^{-1}}\left( \dfrac{\text{Hypotenuse }}{\text{Base}} \right)$ ………………………………………..(iii)
Now, we can draw a right angle triangle with the help of expression ${{\sec }^{-1}}x$ inside tan of equation (ii) and using equation (iii) as well.
So, we can suppose angle $\theta$ in a right angle triangle using relation
$\theta ={{\sec }^{-1}}\left( \dfrac{x}{1} \right)$ ……………………………………(iv)
Hence, a right angled triangle with Hypotenuse $=x$ and Base $=1$ can be drawn as

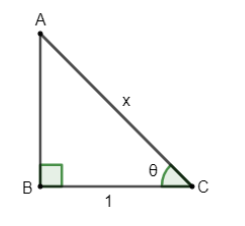
Now, as we know the Pythagoras theorem for a right angled triangle is given as: -
${{\left( \text{Hypotenuse} \right)}^{2}}={{\left( \text{Base} \right)}^{2}}+{{\left( \text{Perpendicular} \right)}^{2}}$ …………………………………….(v)
So, we get the above equation with help of $\Delta ABC$ as
$\Rightarrow {{\left( AC \right)}^{2}}={{\left( BC \right)}^{2}}+{{\left( AB \right)}^{2}}$
$\Rightarrow {{x}^{2}}={{1}^{2}}+{{\left( AB \right)}^{2}}$
$\Rightarrow {{\left( AB \right)}^{2}}={{x}^{2}}-1$
Taking square root to both the sides, we get
$\Rightarrow AB=\sqrt{{{x}^{2}}-1}$
Now, as we know $\tan \theta =\dfrac{\text{Perpendicular}}{\text{Base}}$
Hence, we get the value of $\tan \theta$ from $\Delta ABC$ as: -
$\Rightarrow \tan \theta =\dfrac{AB}{BC}=\dfrac{\sqrt{{{x}^{2}}-1}}{1}$
$\Rightarrow \theta ={{\tan }^{-1}}\left( \sqrt{{{x}^{2}}-1} \right)$ ………………………………..(vi)
Now, we can get from equation (iv) and (vi) that
${{\sec }^{-1}}x={{\tan }^{-1}}\left( \sqrt{{{x}^{2}}-1} \right)$
Hence, equation (ii) can be written as
$\Rightarrow LHS=\tan \left( {{\tan }^{-1}}\sqrt{{{x}^{2}}-1} \right)$ ………………………………………(vii)
Now, as we know $\tan \left( {{\tan }^{-1}}\theta \right)=\theta$ …………………………………….(viii)
Hence, we get equation (vii) as
LHS $=\sqrt{{{x}^{2}}-1}$ ………………………………….(ix)
Now, RHS of the equation (i) is given as
$\Rightarrow RHS=\sin \left( {{\cos }^{-1}}\left( \dfrac{1}{\sqrt{5}} \right) \right)$ ……………………………………(x)
Now, as we know $\cos \theta =\dfrac{Base}{Hypotenuse}$ $\Rightarrow \theta ={{\cos }^{-1}}\left( \dfrac{Base}{Hypotenuse} \right)$ …………………….(xi)
So, on comparing the above equation with the term ${{\cos }^{-1}}\left( \dfrac{1}{\sqrt{5}} \right)$ inside the function sin of the equation (x). We get $\theta ={{\cos }^{-1}}\left( \dfrac{1}{\sqrt{5}} \right)$ …………………………….(xii)
So, we can draw right angle triangle with Base $=1$, Hypotenuse $=\sqrt{5}$
Hence, we can draw a triangle as

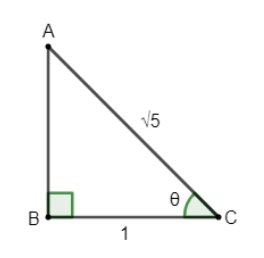
Now, using equation (v), we get
$\Rightarrow {{\left( AC \right)}^{2}}={{\left( AB \right)}^{2}}+{{\left( BC \right)}^{2}}$
$\Rightarrow {{\left( \sqrt{5} \right)}^{2}}={{\left( AB \right)}^{2}}+1$
$\Rightarrow {{\left( AB \right)}^{2}}=5-1=4$
$\Rightarrow AB=2$
Hence, we know $\sin \theta$ is defined as $\sin \theta =\dfrac{\text{Perpendicular}}{\text{Hypotenuse}}=\dfrac{AB}{AC}$
$\sin \theta =\dfrac{2}{\sqrt{5}}$ $\Rightarrow \theta ={{\sin }^{-1}}\left( \dfrac{2}{\sqrt{5}} \right)$ ………………………………(xiii)
Hence, we can rewrite equation (x) using equation (xii) and (xiii) as
RHS $=\sin \left( {{\sin }^{-1}}\left( \dfrac{2}{\sqrt{5}} \right) \right)$
Now, as we know $\sin \left( {{\sin }^{-1}}\theta \right)=\theta$
So, we get RHS $=\dfrac{2}{\sqrt{5}}$ ……………………………………..(xiv)
Now, we can rewrite equation (i) using equations (ix) and (xiv) as
$\Rightarrow \sqrt{{{x}^{2}}-1}=\dfrac{2}{\sqrt{5}}$
On squaring both the sides of the above equation, we get
$\Rightarrow {{x}^{2}}-1=\dfrac{4}{5}$
$\Rightarrow {{x}^{2}}=1+\dfrac{4}{5}=\dfrac{9}{5}$
$\Rightarrow {{x}^{2}}=\dfrac{9}{5}$
Taking square root on both the sides of the above equation, we get
$\Rightarrow x=\pm \dfrac{3}{\sqrt{5}}$
Hence, option (a) is the correct answer.

Note: One need to be careful with the identities $\tan \left( {{\tan }^{-1}}x \right)=x$ and $\sin \left( {{\sin }^{-1}}x \right)=x$. One may confuse with the identities of $\sin \left( {{\sin }^{-1}}x \right)$ and $\tan \left( {{\tan }^{-1}}x \right)$ which will not always be x. So, be careful with them. Don’t confuse yourself with these relations.
One may use direct identities to convert ${{\sec }^{-1}}x$ to ${{\tan }^{-1}}$ and ${{\cos }^{-1}}$ function to ${{\sin }^{-1}}$ . These are given as
${{\sec }^{-1}}x={{\tan }^{-1}}\sqrt{{{x}^{2}}-1}$
${{\cos }^{-1}}x={{\sin }^{-1}}\sqrt{1-{{x}^{2}}}$
So, we do not need to make a right angle triangle to get solve the problem instead, we can use the above identities as well.