Question

If $\tan \alpha =\dfrac{p}{q}$ , where $\alpha =6\beta$ , $\alpha$ being an acute angle, prove that : \dfrac{1}{2}\left\\{ p\operatorname{cosec}2\beta -q\sec 2\beta \right\\}=\sqrt{{{p}^{2}}+{{q}^{2}}} .

Answer 1

To prove the above equation, first you need to convert $\operatorname{cosec}2\beta$ and $\sec 2\beta$ into $\sin 2\beta$ and $\cos 2\beta$ , using the identity $\sin \theta =\dfrac{1}{\operatorname{cosec}\theta }$ and $\cos \theta =\dfrac{1}{\sec \theta }$ . Then, use the identity $\sin 2\theta =2\sin \theta \cos \theta$ and multiply numerator and denominator with $\sqrt{{{p}^{2}}+{{q}^{2}}}$ and use triangle law of trigonometry and write $\sin \alpha =\dfrac{p}{\sqrt{{{p}^{2}}+{{q}^{2}}}}$ and $\cos \alpha =\dfrac{q}{\sqrt{{{p}^{2}}+{{q}^{2}}}}$ .Now, use formula $\sin \left( A-B \right)=\sin A\cos B-\sin B\cos A$ and put $\alpha =6\beta$ .

Complete step-by-step answer:
Since, we known that $\sin \theta =\dfrac{1}{\operatorname{cosec}\theta }$ and $\cos \theta =\dfrac{1}{\sec \theta }$ , then we can write LHS of the above equation \dfrac{1}{2}\left\\{ p\operatorname{cosec}2\beta -q\sec 2\beta \right\\}=\sqrt{{{p}^{2}}+{{q}^{2}}} as:
=\dfrac{1}{2}\left\\{ \dfrac{p}{\sin 2\beta }-\dfrac{q}{\cos 2\beta } \right\\}
Take LCM of $\sin 2\beta$ and $\cos 2\beta$ , then we will get:
=\dfrac{1}{2}\left\\{ \dfrac{p\cos 2\beta -q\sin 2\beta }{\sin 2\beta \cos 2\beta } \right\\}
$=\dfrac{p\cos 2\beta -q\sin 2\beta }{2\sin 2\beta \cos 2\beta }$
We know that $\sin 2\theta =2\sin \theta \cos \theta$ , hence we will get
$=\dfrac{p\cos 2\beta -q\sin 2\beta }{\sin 4\beta }$
Now, we will multiply numerator and denominator with $\sqrt{{{p}^{2}}+{{q}^{2}}}$ , we will get:
=\dfrac{\sqrt{{{p}^{2}}+{{q}^{2}}}}{\sin 4\beta }\left\\{ \dfrac{p\cos 2\beta -q\sin 2\beta }{\sqrt{{{p}^{2}}+{{q}^{2}}}} \right\\}
Now, split $\sqrt{{{p}^{2}}+{{q}^{2}}}$ over both the numerator term:
=\dfrac{\sqrt{{{p}^{2}}+{{q}^{2}}}}{\sin 4\beta }\left\\{ \dfrac{p\cos 2\beta }{\sqrt{{{p}^{2}}+{{q}^{2}}}}-\dfrac{q\sin 2\beta }{\sqrt{{{p}^{2}}+{{q}^{2}}}} \right\\}............\left( 1 \right)
Now, we will use triangle law of trigonometry (i.e. $\sin \theta =\dfrac{perpendicular}{hypotenuse}$ , $\cos \theta =\dfrac{base}{hypotenuse}$ and $\tan \theta =\dfrac{perpendicular}{base}$)
It is given in question that $\tan \alpha =\dfrac{p}{q}$ , hence perpendicular of the triangle is ‘p’ and its base is ‘q’, then, the hypotenuse will become $\sqrt{{{p}^{2}}+{{q}^{2}}}$ , so we can draw the below diagram:

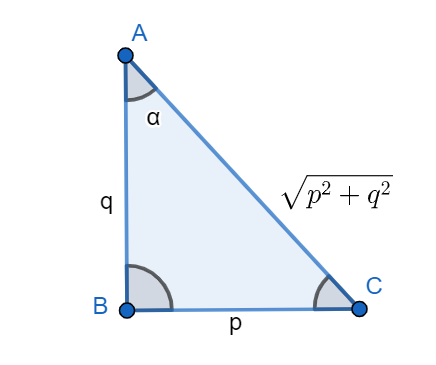
From the figure, it can be seen that we can write $\sin \alpha =\dfrac{p}{\sqrt{{{p}^{2}}+{{q}^{2}}}}$ and $\cos \alpha =\dfrac{q}{\sqrt{{{p}^{2}}+{{q}^{2}}}}$ .
Hence, the above equation (1) will become:
=\dfrac{\sqrt{{{p}^{2}}+{{q}^{2}}}}{\sin 4\beta }\left\\{ \sin \alpha \cos 2\beta -\cos \alpha \sin 2\beta \right\\}
Now, by using the formula $\sin \left( A-B \right)=\sin A\cos B-\sin B\cos A$ , we can rewrite the above equation as:
$=\dfrac{\sqrt{{{p}^{2}}+{{q}^{2}}}}{\sin 4\beta }\sin \left( \alpha -2\beta \right)$
Now, we will put $\alpha =6\beta$ in the above equation, then we will get:
$=\dfrac{\sqrt{{{p}^{2}}+{{q}^{2}}}}{\sin 4\beta }\sin \left( 6\beta -2\beta \right)$
$=\dfrac{\sqrt{{{p}^{2}}+{{q}^{2}}}}{\sin 4\beta }\sin \left( 4\beta \right)$
$=\sqrt{{{p}^{2}}+{{q}^{2}}}$ = RHS
Hence, LHS = RHS
This is our required proof.

Note: Students are required to check that weather $\alpha$ is an acute angle or not, otherwise there is chance of change of sign while writing $\sin \alpha =\dfrac{p}{\sqrt{{{p}^{2}}+{{q}^{2}}}}$ and $\cos \alpha =\dfrac{q}{\sqrt{{{p}^{2}}+{{q}^{2}}}}$ , if $\alpha$ become greater than $90{}^\circ$ .