Question

If tan A and tan B are the roots of the quadratic equation $ab{x^2} - {c^2}x + ab = 0$ , where a, b, c are the sides of the triangle ABC, then prove ${\sin ^2}A + {\sin ^2}B + {\sin ^2}C = 2$

Answer 1

Hint : We can use the sum and product of roots, identity for sum of tan of angles and calculate the various angles of triangle ABC. We can then find the sine for these angles and add their squares to prove the given equation.
Formulas to be used:
$S = \dfrac{{Coeff.{\text{ }}of{\text{ }}x}}{{const.}} \\\ P = \dfrac{{Coeff.{\text{ }}of{\text{ }}{x^2}}}{{const.}} \\\$ where, S and P are sum and products of the roots of a quadratic equation
$\tan (A + B) = \dfrac{{\tan A + \tan B}}{{1 - \tan A \times \tan B}}$
$\sin \theta = \dfrac{{perpendicular}}{{hypotenuse}}$
According to Pythagoras theorem:
${H^2} = {P^2} + {B^2}$ where, H is hypotenuse, P is perpendicular and B is the base for the right angled triangle.

Complete step-by-step answer :
It is given that tan A and tan B are the roots of the quadratic equation $ab{x^2} - {c^2}x + ab = 0$ .
The sum of and product of the roots of a quadratic equation are given as:
$S = \dfrac{{Coeff.{\text{ }}of{\text{ }}x}}{{const.}} \\\ P = \dfrac{{Coeff.{\text{ }}of{\text{ }}{x^2}}}{{const.}} \;$
For the given quadratic equation:
$\tan A + \tan B = \dfrac{{{c^2}}}{{ab}} \\\ \tan A \times \tan B = \dfrac{{ab}}{{ab}} = 1 \\\$
From the identity of sum of angles of tan:
$\tan (A + B) = \dfrac{{\tan A + \tan B}}{{1 - \tan A \times \tan B}}$
Substituting the values, we get:
$\tan (A + B) = \dfrac{{\dfrac{{{c^2}}}{{ab}}}}{{1 - 1}} \\\ \tan (A + B) = \dfrac{{\dfrac{{{c^2}}}{{ab}}}}{0} \\\ \Rightarrow \tan (A + B) = \infty \\\ \Rightarrow \tan (A + B) = \tan \dfrac{\pi }{2}\left( {\because \tan \dfrac{\pi }{2} = \infty } \right) \;$
We can now get the value of the angles of the triangle ABC.
$A + B = \dfrac{\pi }{2}$
Sum of all the three angles in a triangle is 180°.
$A + B + C = {180^\circ } \\\ \Rightarrow \dfrac{\pi }{2} + C = {180^\circ } \\\ \Rightarrow C = {180^\circ } - {90^\circ }\left( {\because \dfrac{\pi }{2} = {{90}^\circ }} \right) \\\ \Rightarrow C = {90^\circ } \;$
So the triangle can be drawn as:

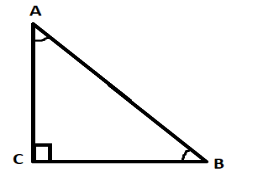
We can calculate the sine of respective angles using the formula for sine.
$\sin \theta = \dfrac{{perpendicular}}{{hypotenuse}}$
$\Rightarrow \sin A = \dfrac{{BC}}{{AB}} \\\ \Rightarrow \sin B = \dfrac{{AC}}{{AB}} \\\ \Rightarrow \sin C = 1\left( {\because \sin 90 = 1} \right) \;$
Now, according to the question we have to prove that ${\sin ^2}A + {\sin ^2}B + {\sin ^2}C = 2$ , so:
${\sin ^2}A + {\sin ^2}B + {\sin ^2}C = \dfrac{{B{C^2}}}{{A{B^2}}} + \dfrac{{A{C^2}}}{{A{B^2}}} + 1 \\\ {\sin ^2}A + {\sin ^2}B + {\sin ^2}C = \dfrac{{B{C^2} + A{C^2}}}{{A{B^2}}} + 1 \;$
From Pythagoras theorem:
${H^2} = {P^2} + {B^2}$ , here,
Hypotenuse (H) = AB
Perpendicular = AC
Base (B) = BC
$\Rightarrow A{B^2} = A{C^2} + B{C^2}$
Substituting this, we get:
${\sin ^2}A + {\sin ^2}B + {\sin ^2}C = \dfrac{{A{B^2}}}{{A{B^2}}} + 1 \\\ {\sin ^2}A + {\sin ^2}B + {\sin ^2}C = 1 + 1 \\\ {\sin ^2}A + {\sin ^2}B + {\sin ^2}C = 2 \;$
Hence, the given statement is proved.

Note : We can apply Pythagoras theorems only on right-angled triangles where one of the angles is of 90°.In a quadratic equation, the maximum degree of a variable is 2, that is how we identify the given equation as quadratic.We can write the angle of 90° or $\dfrac{\pi }{2}$ according to the needs, both representing the same measure of angle.
The perpendicular side for an angle is the side opposite to it.