Question

If T be any point on the tangent at any point P of a parabola, and if TL be perpendicular to the focal radius SP and TN be perpendicular to the directrix, then prove that SL=TN.
Hence obtain a geometric construction for the pair of tangents drawn to the parabola from any point T.

Answer 1

First, before proceeding for this, we must know that the equation of the parabola be ${{y}^{2}}=4ax$ and point P be at $\left( a{{t}^{2}},2at \right)$ and point T be $\left( h,k \right)$. Then, we know that the equation of tangent at P is given by $ty=h+a{{t}^{2}}$. Then, we are given the condition that TL is perpendicular to SP to get the value of Sp and similarly we get the value of TN by its perpendicular condition and get the condition proved as required.

Complete step-by-step answer :
In this question, we are supposed to obtain a geometric construction for the pair of tangents drawn to the parabola from any point T where T be any point on the tangent at any point P of a parabola, and if TL be perpendicular to the focal radius SP and TN be perpendicular to the directrix, then prove that SL=TN.
So, before proceeding for this, we must know that the equation of the parabola be ${{y}^{2}}=4ax$ and point P be at $\left( a{{t}^{2}},2at \right)$ and point T be $\left( h,k \right)$.

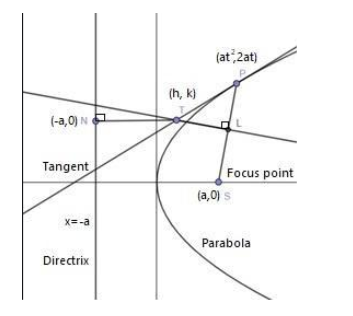
Then, we know that the equation of tangent at P is given by:
$ty=h+a{{t}^{2}}.....\left( i \right)$
Then, we get the slope m of the parabola SP is given by:
$\begin{aligned} & m=\dfrac{2at-0}{a{{t}^{2}}-a} \\\ & \Rightarrow m=\dfrac{2at}{a{{t}^{2}}-a} \\\ & \Rightarrow m=\dfrac{2t}{{{t}^{2}}-1} \\\ \end{aligned}$
Then, we are given with the condition that TL is perpendicular to SP.
So, by using this condition, we get the equation of TL as:
$2ty+\left( {{t}^{2}}-1 \right)x-2kt-\left( {{t}^{2}}-1 \right)h=0....\left( ii \right)$
Now, we need to find the perpendicular distance of S(a, 0) from the equation (ii), we get:
$\begin{aligned} & SL=\dfrac{\left| \left( {{t}^{2}}-1 \right)x-2kt-\left( {{t}^{2}}-1 \right)h \right|}{\sqrt{4{{t}^{2}}+{{\left( {{t}^{2}}-1 \right)}^{2}}}} \\\ & \Rightarrow SL=\dfrac{\left| -h-h{{t}^{2}}-a-a{{t}^{2}} \right|}{\sqrt{{{\left( {{t}^{2}}+1 \right)}^{2}}}} \\\ & \Rightarrow SL=\dfrac{\left( a+h \right)\left( {{t}^{2}}+1 \right)}{\left( {{t}^{2}}+1 \right)} \\\ & \Rightarrow SL=\left( a+h \right).....\left( iii \right) \\\ \end{aligned}$
So, we get the value of SL as (a+h).
Then, we get the equation of the directrix as:
$x=-a....\left( iv \right)$
Now, we are also given in the question that TN is perpendicular with coordinates as (h, k) to equation (iv), we get:
$TN=\dfrac{h\left( 1 \right)+k\left( 0 \right)+a}{\sqrt{{{1}^{2}}+{{0}^{2}}}}$
So, by solving the above expression, we get:
$TN=h+a....\left( v \right)$
Now, from equation (iii) and (v), we can see that they both are equal.
So, we can conclude that SL=TN.
Hence, the given condition is proved.

Note : Now, to solve these types of the questions we need to know some of the basic formulas for the equation of the parabolas. So, some of the basic equations of the parabola are as:
The general equation of the parabola is as ${{\left( y-k \right)}^{2}}=4a\left( x-h \right)$ where (h, k) is the vertex.
The equation of directrix of parabola is given by $x-h+a=0$.
The equation of the axis which is in general given by $y-k=0$.