Question

If ‘T’ be any point on a tangent at any point ‘P’ of a parabola, and if TL is perpendicular to focal radius SP and TN is perpendicular to directrix, prove that $SL=TN$

Answer 1

We solve this problem first by drawing the figure of given data as follows

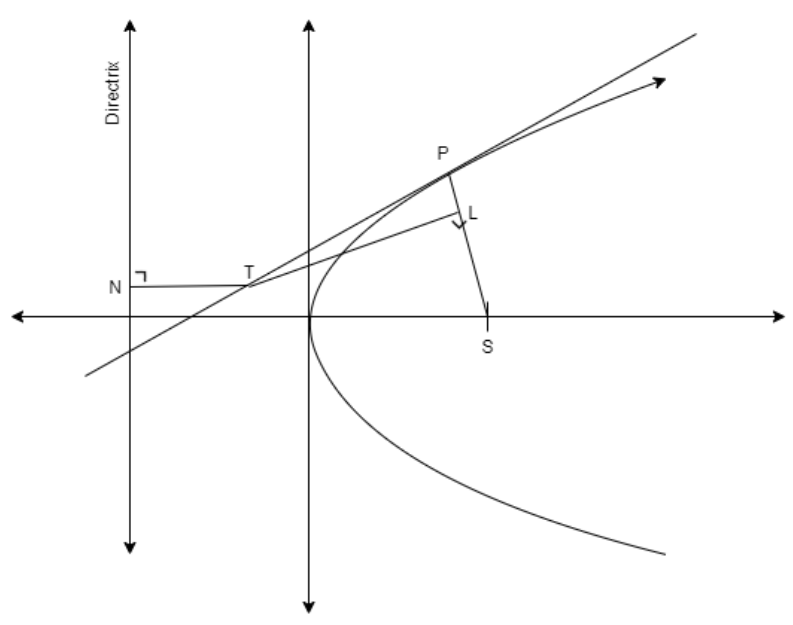
Here, we assume the parabola equation as ${{y}^{2}}=4ax$ and the point ‘T’ as $\left( h,k \right)$ also we use the parametric point form of P as $\left( 2at,a{{t}^{2}} \right)$ then we find the equations of lines ‘TL’ and directrix to find the perpendicular distances SL and TN to show that both are equal.

Complete step-by-step solution:
Let us assume that the equation of parabola as
$\Rightarrow {{y}^{2}}=4ax$
We know that the parametric point of a parabola is given as $\left( 2at,a{{t}^{2}} \right)$
Let us assume that the point P as
$\Rightarrow P=\left( 2at,a{{t}^{2}} \right)$
We know that the focus point of parabola is $S\left( a,0 \right)$
Now, let us find the slope of line SP
We know that the slope of two points $\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)$ is given as
$\Rightarrow m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$
By using the above formula we get the slope of SP as

& \Rightarrow {{m}_{1}}=\dfrac{2at-0}{a{{t}^{2}}-a} \\\ & \Rightarrow {{m}_{1}}=\dfrac{2t}{{{t}^{2}}-1} \\\ \end{aligned}$$ Now, let us find the slope of line TL We are given that $$TL\bot SP$$ We know that when two lines are perpendicular then the product of slopes equal to -1 So, is the slope of TL is $${{m}_{2}}$$ then we can write $$\begin{aligned} & \Rightarrow {{m}_{1}}\times {{m}_{2}}=-1 \\\ & \Rightarrow {{m}_{2}}=-\dfrac{1}{{{m}_{1}}} \\\ \end{aligned}$$ By substituting the slope of SP we get $$\begin{aligned} & \Rightarrow {{m}_{2}}=-\left( \dfrac{{{t}^{2}}-1}{2t} \right) \\\ & \Rightarrow {{m}_{2}}=\dfrac{1-{{t}^{2}}}{2t} \\\ \end{aligned}$$ Now, let us assume that the point T as $$\left( h,k \right)$$ Here, we have the slope of line TL and one point T then by using the slope point form the equation of line TL can be written as $$\Rightarrow y-k={{m}_{2}}\left( x-h \right)$$ By substituting the slope in the above equation we get $$\Rightarrow y-k=\dfrac{1-{{t}^{2}}}{2t}\left( x-h \right)$$ By cross multiplying the above equation we get $$\begin{aligned} & \Rightarrow 2ty-2tk=x\left( 1-{{t}^{2}} \right)-h\left( 1-{{t}^{2}} \right) \\\ & \Rightarrow x\left( 1-{{t}^{2}} \right)-2yt+2tk-h\left( 1-{{t}^{2}} \right)=0........equation(i) \\\ \end{aligned}$$ Now, let us find the length of SL We know that the perpendicular distance from point $$\left( {{x}_{1}},{{y}_{1}} \right)$$ to the line $$ax+by+c=0$$ is given as $$\Rightarrow D=\dfrac{\left| a{{x}_{1}}+b{{y}_{1}}+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$$ Here, we know that the length SL is perpendicular distance from focus $$S\left( a,0 \right)$$ to line TL By using the above perpendicular distance formula we get $$\Rightarrow SL=\dfrac{\left| a\left( 1-{{t}^{2}} \right)+2tk-h\left( 1-{{t}^{2}} \right) \right|}{\sqrt{{{\left( 1-{{t}^{2}} \right)}^{2}}+{{\left( 2t \right)}^{2}}}}$$ We know that the equation of tangent at a parametric point $$P\left( a{{t}^{2}},2at \right)$$ is given as $$\Rightarrow ty=x+a{{t}^{2}}$$ We are given that this equation of tangent passes through point $$T\left( h,k \right)$$ then we get $$\Rightarrow tk=h+a{{t}^{2}}$$ Now, by substituting the above result in the distance of SL we get $$\begin{aligned} & \Rightarrow SL=\dfrac{\left| a-a{{t}^{2}}+2h+2a{{t}^{2}}-h+h{{t}^{2}} \right|}{\sqrt{{{\left( 1+{{t}^{2}} \right)}^{2}}}} \\\ & \Rightarrow SL=\dfrac{\left( a+h \right)\left( 1+{{t}^{2}} \right)}{\left( 1+{{t}^{2}} \right)} \\\ & \Rightarrow SL=a+h......equation(ii) \\\ \end{aligned}$$ Now, let us find the length of TN We know that the equation of directrix of parabola $${{y}^{2}}=4ax$$ is given as $$\Rightarrow x+a=0$$ Here, we can see that the length TN is the perpendicular distance from point $$T\left( h,k \right)$$ to directrix because we are given that TN is perpendicular to directrix. Now, by using the perpendicular distance formula we get $$\begin{aligned} & \Rightarrow TN=\dfrac{\left| h+a \right|}{\sqrt{{{1}^{2}}+{{0}^{2}}}} \\\ & \Rightarrow TN=h+a.......equation(iii) \\\ \end{aligned}$$ Now, from the equation (ii) and equation (iii) we get $$\Rightarrow SL=TN$$ Therefore, the required result has been proved. **Note:** Here we used the general type of parabola but we can use any type of parabola to get the required result. For the parabola $${{y}^{2}}=4ax$$ we used some standard formulas such as (i) Parametric point is given as $$\left( 2at,a{{t}^{2}} \right)$$ (ii) Equation of tangent at any point $$\left( 2at,a{{t}^{2}} \right)$$ is given as $$\Rightarrow ty=x+a{{t}^{2}}$$ (iii) Directrix is given as $$\Rightarrow x+a=0$$ (iv) The perpendicular distance from point $$\left( {{x}_{1}},{{y}_{1}} \right)$$ to the line $$ax+by+c=0$$ is given as $$\Rightarrow D=\dfrac{\left| a{{x}_{1}}+b{{y}_{1}}+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$$ These are important results to be remembered while solving this problem.