Question

If $\sum_{r=0}^{3n} a_r (x-4)^r = \sum_{r=0}^{3n} A_r (x-5)^r$ and $a_k = 1 \forall K \ge 2n$ and $\sum_{r=0}^{3n} d_r (x-8)^r = \sum_{r=0}^{3n} B_r (x-9)^r$ and $\sum_{r=0}^{3n} d_r (x-12)^r = \sum_{r=0}^{3n} D_r (x-13)^r$ and $d_k = 1 \forall K \ge 2n$. The find the value of $\frac{A_{2n}+D_{2n}}{B_{2n}}$.

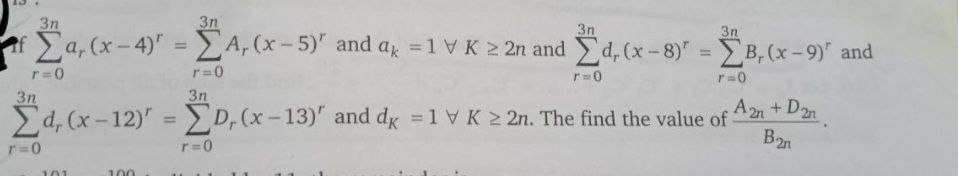
• A. 1
• B. 2
• C. 3
• D. 4

Answer 1

Answer: (B)

2

Answer 2

Let $P(x) = \sum_{r=0}^{3n} a_r (x-c)^r$. If we expand $P(x)$ in powers of $(x-d)$, say $P(x) = \sum_{k=0}^{3n} C_k (x-d)^k$, then the coefficients $C_k$ are related to $a_r$ by the formula: $C_k = \sum_{r=k}^{3n} a_r \binom{r}{k} (d-c)^{r-k}$.

For the first identity: $\sum_{r=0}^{3n} a_r (x-4)^r = \sum_{r=0}^{3n} A_r (x-5)^r$. Here, $c=4$, $a_r$ are the coefficients of $(x-4)^r$, and $d=5$, $A_k$ are the coefficients of $(x-5)^k$. $A_k = \sum_{r=k}^{3n} a_r \binom{r}{k} (5-4)^{r-k} = \sum_{r=k}^{3n} a_r \binom{r}{k}$. Given $a_k = 1$ for $k \ge 2n$. To find $A_{2n}$: $A_{2n} = \sum_{r=2n}^{3n} a_r \binom{r}{2n} = \sum_{r=2n}^{3n} 1 \cdot \binom{r}{2n}$. Using the hockey-stick identity $\sum_{i=k}^m \binom{i}{k} = \binom{m+1}{k+1}$: $A_{2n} = \binom{3n+1}{2n+1}$.

For the second identity: $\sum_{r=0}^{3n} d_r (x-8)^r = \sum_{r=0}^{3n} B_r (x-9)^r$. $B_k = \sum_{r=k}^{3n} d_r \binom{r}{k} (9-8)^{r-k} = \sum_{r=k}^{3n} d_r \binom{r}{k}$. Given $d_k = 1$ for $k \ge 2n$. To find $B_{2n}$: $B_{2n} = \sum_{r=2n}^{3n} d_r \binom{r}{2n} = \sum_{r=2n}^{3n} 1 \cdot \binom{r}{2n}$. $B_{2n} = \binom{3n+1}{2n+1}$.

For the third identity: $\sum_{r=0}^{3n} d_r (x-12)^r = \sum_{r=0}^{3n} D_r (x-13)^r$. $D_k = \sum_{r=k}^{3n} d_r \binom{r}{k} (13-12)^{r-k} = \sum_{r=k}^{3n} d_r \binom{r}{k}$. Given $d_k = 1$ for $k \ge 2n$. To find $D_{2n}$: $D_{2n} = \sum_{r=2n}^{3n} d_r \binom{r}{2n} = \sum_{r=2n}^{3n} 1 \cdot \binom{r}{2n}$. $D_{2n} = \binom{3n+1}{2n+1}$.

The required value is $\frac{A_{2n}+D_{2n}}{B_{2n}} = \frac{\binom{3n+1}{2n+1} + \binom{3n+1}{2n+1}}{\binom{3n+1}{2n+1}} = \frac{2 \binom{3n+1}{2n+1}}{\binom{3n+1}{2n+1}} = 2$.