Question

If $\sum_{n=1}^{49}\frac{1}{\sqrt{n+\sqrt{n^2-1}}}=a+b\sqrt{2}$, if "a & b" are natural numbers then

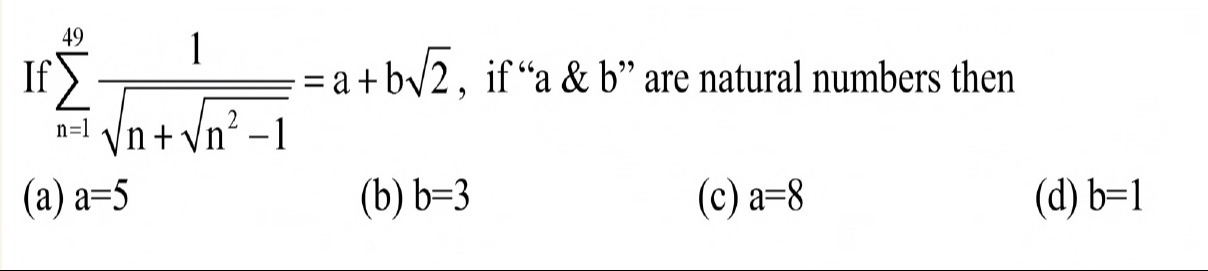
• A. a=5
• B. b=3
• C. a=8
• D. b=1

Answer 1

Answer: (A), (B)

a=5, b=3

Answer 2

The general term $\frac{1}{\sqrt{n+\sqrt{n^2-1}}}$ simplifies to $\frac{1}{\sqrt{2}}(\sqrt{n+1} - \sqrt{n-1})$. The sum becomes a telescoping series $\frac{1}{\sqrt{2}} \sum_{n=1}^{49} (\sqrt{n+1} - \sqrt{n-1})$. Evaluating this sum yields $5 + 3\sqrt{2}$. Comparing with $a+b\sqrt{2}$, we get $a=5$ and $b=3$.