Question
Question: If sum of first n terms of an A.P. is (3n$^2$ – 2n) ∀ n ∈ N, then the value of $\sum_{n=1}^{\infty} ...
If sum of first n terms of an A.P. is (3n2 – 2n) ∀ n ∈ N, then the value of ∑n=1∞(SnSn+2+Sn−1Sn+1)−(SnSn+1+Sn−1Sn+2)21 is
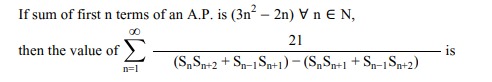
2
Solution
The sum of the first n terms of an A.P. is given by Sn=3n2−2n for all n∈N. The n-th term of the A.P. is an=Sn−Sn−1 for n>1, and a1=S1.
S1=3(1)2−2(1)=1. So a1=1.
For n>1, Sn−1=3(n−1)2−2(n−1)=3(n2−2n+1)−2n+2=3n2−6n+3−2n+2=3n2−8n+5.
an=(3n2−2n)−(3n2−8n+5)=6n−5.
This formula also works for n=1: a1=6(1)−5=1. So the general term of the A.P. is an=6n−5. The common difference of the A.P. is d=an+1−an=(6(n+1)−5)−(6n−5)=6n+6−5−6n+5=6.
The expression in the denominator of the sum term is (SnSn+2+Sn−1Sn+1)−(SnSn+1+Sn−1Sn+2). Let's simplify this expression: Dn=SnSn+2+Sn−1Sn+1−SnSn+1−Sn−1Sn+2 Dn=(SnSn+2−SnSn+1)−(Sn−1Sn+2−Sn−1Sn+1) Dn=Sn(Sn+2−Sn+1)−Sn−1(Sn+2−Sn+1) Dn=(Sn−Sn−1)(Sn+2−Sn+1).
We know that Sk−Sk−1=ak for k≥2. So Sn−Sn−1=an for n≥2. And Sn+2−Sn+1=an+2 for n+2≥2, which means n≥0. Since n∈N, this holds for n≥1. For n≥2, Dn=anan+2.
For n=1, the expression involves Sn−1=S0. The formula Sn=3n2−2n gives S0=3(0)2−2(0)=0. Assuming S0=0, the denominator for n=1 is: D1=(S1S3+S0S2)−(S1S2+S0S3)=(S1S3+0)−(S1S2+0)=S1(S3−S2). S1=1. a2=6(2)−5=7. a3=6(3)−5=13. S2=S1+a2=1+7=8. S3=S2+a3=8+13=21. D1=S1(S3−S2)=1(21−8)=1×13=13. The formula anan+2 for n=1 gives a1a3=1×13=13. Thus, the denominator is Dn=anan+2 for all n≥1.
The sum is ∑n=1∞anan+221. Substitute an=6n−5 and an+2=6(n+2)−5=6n+12−5=6n+7. The term is (6n−5)(6n+7)21.
We use partial fraction decomposition: (6n−5)(6n+7)21=6n−5A+6n+7B. 21=A(6n+7)+B(6n−5). Setting 6n−5=0⟹n=5/6, we get 21=A(6(5/6)+7)=A(5+7)=12A⟹A=21/12=7/4. Setting 6n+7=0⟹n=−7/6, we get 21=B(6(−7/6)−5)=B(−7−5)=−12B⟹B=21/(−12)=−7/4. So (6n−5)(6n+7)21=6n−57/4−6n+77/4=47(6n−51−6n+71). Recognizing an=6n−5 and an+2=6n+7, the term is 47(an1−an+21).
The sum is ∑n=1∞47(an1−an+21). This is a telescoping series. Let's consider the partial sum SN=∑n=1N47(an1−an+21). SN=47[(a11−a31)+(a21−a41)+(a31−a51)+⋯+(aN−11−aN+11)+(aN1−aN+21)]. The terms cancel out, leaving: SN=47[a11+a21−aN+11−aN+21].
To find the sum of the infinite series, we take the limit as N→∞: ∑n=1∞anan+221=limN→∞SN=47limN→∞[a11+a21−aN+11−aN+21]. As N→∞, aN+1=6(N+1)−5=6N+1→∞ and aN+2=6(N+2)−5=6N+7→∞. So limN→∞aN+11=0 and limN→∞aN+21=0. The sum is 47(a11+a21−0−0)=47(11+71).
We have a1=1 and a2=7. The sum is 47(11+71)=47(1+71)=47(77+1)=47×78=48=2.
The final answer is 2.
Explanation of the solution:
- Find the general term an of the A.P. from the given sum formula Sn. an=Sn−Sn−1 for n>1 and a1=S1.
- Simplify the denominator of the term in the sum. It simplifies to (Sn−Sn−1)(Sn+2−Sn+1).
- Use the relation Sk−Sk−1=ak to express the denominator in terms of the terms of the A.P. The denominator is anan+2 for n≥1 (assuming S0=0, which is consistent with the formula for Sn).
- Substitute the formula for an into the term anan+221.
- Use partial fraction decomposition to rewrite the term anan+221 in the form C(an1−an+21).
- Evaluate the infinite sum using the telescoping series property. The partial sum ∑n=1N(an1−an+21) simplifies to a11+a21−aN+11−aN+21.
- Take the limit of the partial sum as N→∞. Since an→∞ as n→∞, the terms aN+11 and aN+21 go to 0.
- Substitute the values of a1 and a2 to get the final sum.
