Question
Question: If $\sqrt{x+y}+\sqrt{y-x}=5$, then $25\frac{d^2y}{dx^2}$ is equal to...
If x+y+y−x=5, then 25dx2d2y is equal to
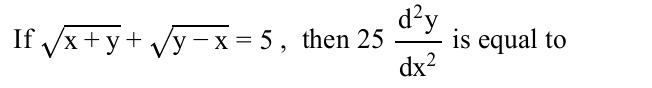
2
Solution
To find 25dx2d2y, we first need to find an explicit expression for y in terms of x from the given equation.
Given equation: x+y+y−x=5
Step 1: Simplify the equation to express y in terms of x. Square both sides of the equation: (x+y+y−x)2=52 Using the identity (a+b)2=a2+b2+2ab: (x+y)+(y−x)+2(x+y)(y−x)=25 2y+2y2−x2=25
Isolate the square root term: 2y2−x2=25−2y
Square both sides again: (2y2−x2)2=(25−2y)2 4(y2−x2)=625−100y+4y2 4y2−4x2=625−100y+4y2
Cancel 4y2 from both sides: −4x2=625−100y
Rearrange the terms to solve for y: 100y=625+4x2 y=100625+4x2 y=100625+1004x2 y=425+25x2
Step 2: Find the first derivative dxdy. Differentiate y=425+25x2 with respect to x: dxdy=dxd(425)+dxd(25x2) dxdy=0+251(2x) dxdy=252x
Step 3: Find the second derivative dx2d2y. Differentiate dxdy=252x with respect to x: dx2d2y=dxd(252x) dx2d2y=252
Step 4: Calculate 25dx2d2y. 25dx2d2y=25×252 25dx2d2y=2
