Question
Question: If slopes of lines represented by $kx^2+5xy+y^2=0$ differ by 1 then $k=...$...
If slopes of lines represented by kx2+5xy+y2=0 differ by 1 then k=...
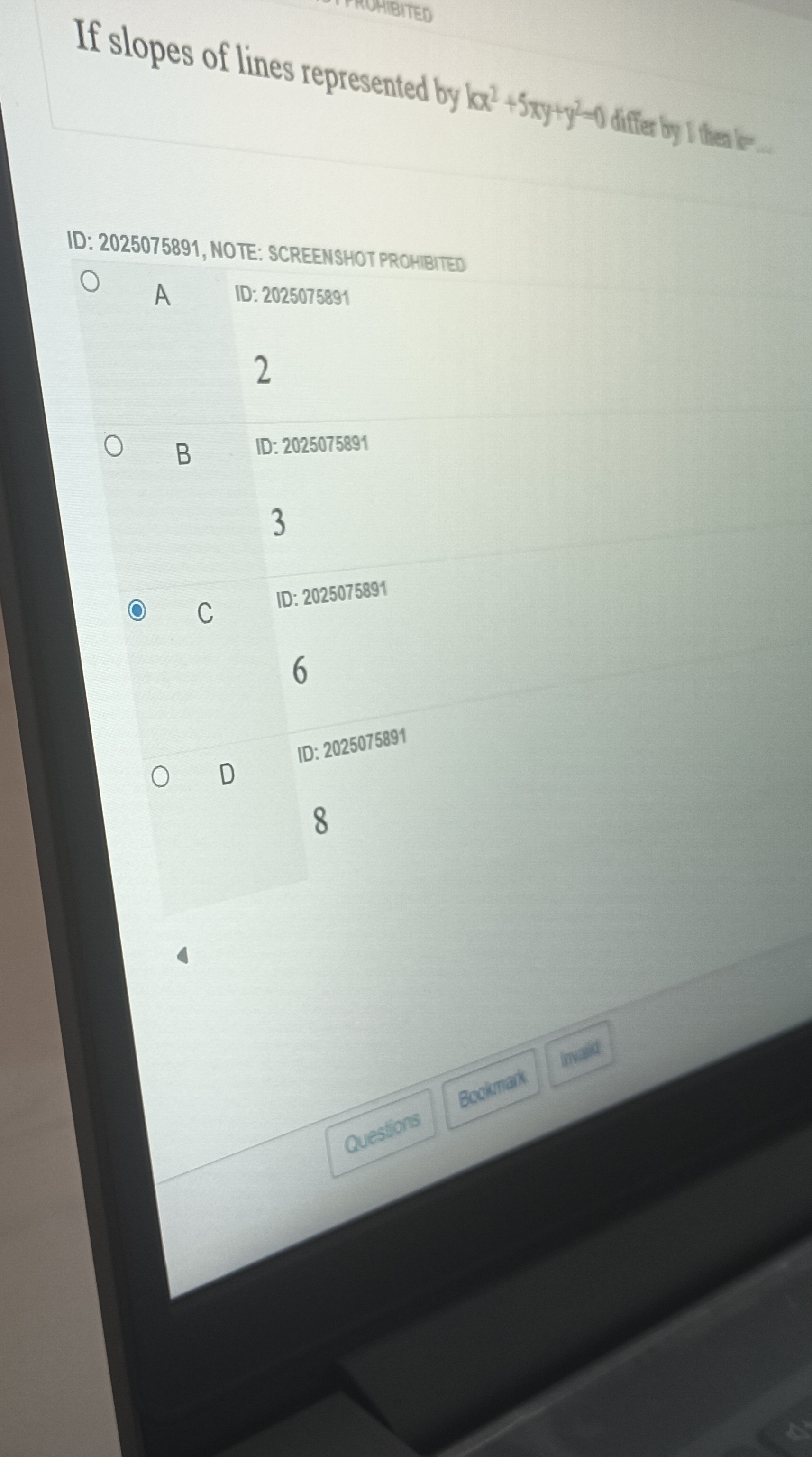
2
3
6
8
6
Solution
The given equation of the pair of straight lines is kx2+5xy+y2=0. This is a homogeneous equation of degree 2, which represents two straight lines passing through the origin. The general form of such an equation is ax2+2hxy+by2=0.
Comparing the given equation with the general form, we have: a=k 2h=5⟹h=25 b=1
Let the slopes of the two lines be m1 and m2. For a pair of straight lines represented by ax2+2hxy+by2=0, the sum and product of the slopes are given by: Sum of slopes: m1+m2=−b2h Product of slopes: m1m2=ba
Substituting the values of a,h,b from our equation: m1+m2=−15=−5 m1m2=1k=k
The problem states that the slopes of the lines differ by 1. This means: ∣m1−m2∣=1
Squaring both sides of this equation: (m1−m2)2=12 (m1−m2)2=1
We know the algebraic identity: (m1−m2)2=(m1+m2)2−4m1m2. Substitute the values from Equation 1 and Equation 2 into this identity: 1=(−5)2−4(k) 1=25−4k
Now, solve for k: 4k=25−1 4k=24 k=424 k=6
Thus, the value of k is 6.
