Question
Question: If $sin(\frac{\pi}{4}cot\theta)=cos(\frac{\pi}{4}tan\theta)$, then $\theta=$...
If sin(4πcotθ)=cos(4πtanθ), then θ=
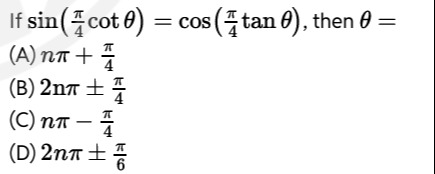
nπ+4π
2nπ±4π
nπ−4π
2nπ±6π
nπ+4π
Solution
The equation sin(4πcotθ)=cos(4πtanθ) can be rewritten using the identity cos(x)=sin(2π−x):
sin(4πcotθ)=sin(2π−4πtanθ)
The general solution for sin(A)=sin(B) is A=nπ+(−1)nB. Let A=4πcotθ and B=2π−4πtanθ.
Case 1: n is even (n=2k). 4πcotθ=2kπ+(2π−4πtanθ) Dividing by 4π: cotθ=8k+2−tanθ cotθ+tanθ=8k+2 sinθcosθ+cosθsinθ=8k+2 sinθcosθcos2θ+sin2θ=8k+2 sinθcosθ1=8k+2 sin(2θ)2=8k+2 sin(2θ)=8k+22=4k+11
For k=0, sin(2θ)=1. The general solution is 2θ=2mπ+2π. θ=mπ+4π. This matches option (A).
Case 2: n is odd (n=2k+1). 4πcotθ=(2k+1)π−(2π−4πtanθ) Dividing by 4π: cotθ=4(2k+1)−2+tanθ cotθ=8k+4−2+tanθ cotθ−tanθ=8k+2 sinθcosθcos2θ−sin2θ=8k+2 sinθcosθcos(2θ)=8k+2 sin(2θ)2cos(2θ)=2(8k+2) 2cot(2θ)=16k+4 cot(2θ)=8k+2 This case does not yield any of the given options.
Checking option (A): If θ=nπ+4π, then tanθ=1 and cotθ=1. LHS = sin(4π×1)=sin(4π)=21. RHS = cos(4π×1)=cos(4π)=21. LHS = RHS, so option (A) is correct.
