Question

If $\sin \theta =\dfrac{8}{17}$, find other trigonometric ratios.

Answer 1

Hint:Assume that in the given function: $\sin \theta =\dfrac{8}{17}$, 8 is the length of perpendicular and 17 is the length of hypotenuse of a right angle triangle. Use Pythagoras theorem given by: $\text{hypotenuse}{{\text{e}}^{\text{2}}}=\text{bas}{{\text{e}}^{\text{2}}}+\text{perpendicular}{{\text{r}}^{\text{2}}}$, to determine the length of the base of the right angle triangle. Now, find $\cos \theta$ by taking the ratio of base and hypotenuse. To find $\tan \theta$ take the ratio of $\sin \theta$ and $\cos \theta$. Take the reciprocal of $\sin \theta$, $\cos \theta$ and $\tan \theta$ to find the value of $\sec \theta$, $\cos ec\theta$ and $\cot \theta$ respectively.

Complete step-by-step answer:
We have been provided with the trigonometric ratio, $\sin \theta =\dfrac{8}{17}$.
We know that, $\sin \theta =\dfrac{\text{Perpendicular}}{\text{Hypotenuse}}$. Therefore, on comparing it with the above provided ratio, we have, 8 as the length of perpendicular and 17 as the length of hypotenuse of a right angle triangle.

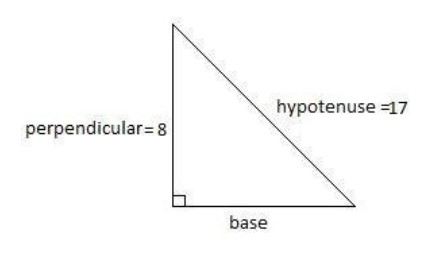
Now, using Pythagoras theorem: $\text{hypotenus}{{\text{e}}^{\text{2}}}=\text{bas}{{\text{e}}^{\text{2}}}+\text{perpendicula}{{\text{r}}^{\text{2}}}$, we get,

& \text{bas}{{\text{e}}^{\text{2}}}=\text{hypotenus}{{\text{e}}^{\text{2}}}-\text{perpendicula}{{\text{r}}^{\text{2}}} \\\ & \Rightarrow \text{base}=\sqrt{\text{hypotenus}{{\text{e}}^{\text{2}}}-\text{perpendicula}{{\text{r}}^{\text{2}}}} \\\ & \Rightarrow \text{base}=\sqrt{{{17}^{\text{2}}}-{{8}^{\text{2}}}} \\\ & \Rightarrow \text{base}=\sqrt{289-64} \\\ & \Rightarrow \text{base}=\sqrt{225} \\\ & \Rightarrow \text{base}=15 \\\ \end{aligned}$$ We know that, $\cos \theta =\dfrac{\text{Base}}{\text{Hypotenuse}}$. $$\Rightarrow \cos \theta =\dfrac{15}{17}$$ Also, $\tan \theta =\dfrac{\text{Perpendicular}}{\text{Base}}$ $\Rightarrow \tan \theta =\dfrac{8}{15}$ Now, take the reciprocal of $\sin \theta $, $\cos \theta $ and $\tan \theta $ to find the value of $\sec \theta $, $\cos ec\theta $ and $\cot \theta $ respectively. $\begin{aligned} & \sec \theta =\dfrac{1}{\cos \theta } \\\ & \Rightarrow \sec \theta =\dfrac{17}{15} \\\ \end{aligned}$ $\begin{aligned} & \cos ec\theta =\dfrac{1}{\sin \theta } \\\ & \Rightarrow \cos ec\theta =\dfrac{17}{8} \\\ \end{aligned}$ $\begin{aligned} & \cot \theta =\dfrac{1}{\tan \theta } \\\ & \Rightarrow \cot \theta =\dfrac{15}{8} \\\ \end{aligned}$ Note: Here, we have used Pythagoras theorem to determine the base of the triangle to find other trigonometric ratios. One may note that, $\sec \theta $ is the ratio of length of hypotenuse and base, $\cos ec\theta $ is the ratio of length of perpendicular and base, and $\cot \theta $ is the ratio of length of base and hypotenuse. So, these ratios can also be found without taking the reciprocals.We can solve the question by using trigonometric identities $\sin^2\theta+\cos^2\theta=1$, $1+\tan^2\theta=\sec^2\theta$ to find all other trigonometric ratios.