Question

If $sin{\text{ }}\theta {\text{ }} = {\text{ }}\dfrac{{12}}{{13}}{\text{ }},{\text{ }}\left( {{\text{ }}0{\text{ }} < {\text{ }}\theta {\text{ }} < {\text{ }}\dfrac{\pi }{2}} \right)$ and $cos{\text{ }}\phi {\text{ }} = {\text{ }}\dfrac{{ - 3}}{5}{\text{ }},{\text{ }}\left( {{\text{ }}\pi {\text{ }} < {\text{ }}\phi {\text{ }} < {\text{ }}\dfrac{{3\pi }}{2}{\text{ }}} \right)$ , then $sin{\text{ }}\left( {{\text{ }}\phi + {\text{ }}\theta {\text{ }}} \right)$ will be
$\left( 1 \right)$ $\dfrac{{ - 56}}{{61}}$
$\;\left( 2 \right)$ $\dfrac{{ - 56}}{{65}}$
$\;\left( 3 \right)$ $\dfrac{1}{{65}}$
$\left( 4 \right)$ $- 56$

Answer 1

Hint : We have to find the value of $sin{\text{ }}\left( {{\text{ }}\phi {\text{ }} + {\text{ }}\theta {\text{ }}} \right)$ . We solve this using the concept of the quadrant system . We should know the concept of sign and value of the trigonometric functions in four quadrants . The values of the trigonometric function have different values for different trigonometric functions with different signs .
We also apply the formula of $sin{\text{ }}\left( {{\text{ }}a{\text{ }} + {\text{ }}b{\text{ }}} \right)$ and putting the values in the required formula we get the value .

Complete step-by-step answer :
$sin{\text{ }}\theta {\text{ }} = \dfrac{{12}}{{13}}{\text{ }},{\text{ }}\left( {{\text{ }}0{\text{ }} < {\text{ }}\theta {\text{ }} < {\text{ }}\dfrac{\pi }{2}{\text{ }}} \right)$
$cos{\text{ }}\phi {\text{ }} = {\text{ }}\dfrac{{ - 3}}{5},{\text{ }}\left( {{\text{ }}\pi {\text{ }} < {\text{ }}\phi < {\text{ }}\dfrac{{3\pi }}{2}} \right)$
The value of $\theta$ lies in the first quadrant
We also know that ,
$sin{\text{ }}\theta {\text{ }} = {\text{ }}\;\dfrac{{{\text{ }}perpendicular}}{{hypotenuse\;}}$
Comparing the two
Perpendicular $\left( {{\text{ }}P{\text{ }}} \right){\text{ }} = {\text{ }}12$ and hypotenuse $\left( {{\text{ }}H{\text{ }}} \right){\text{ }} = {\text{ }}13$

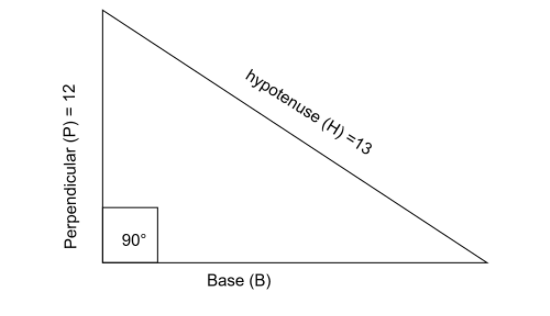
Using the formula ,
${(base)^2} + {(P)^2} = {(H)^2}$
So ,
Value of base $\left( {{\text{ }}B{\text{ }}} \right)$ $= \sqrt {[{H^2} - {P^2}] }$
$B = \sqrt {[{{13}^2} - {{12}^2}] }$
$B = \sqrt {[169 - 144] }$
$B = \sqrt {[25] }$
$B{\text{ }} = {\text{ }}5$
As the value of cos is positive in first quadrant , then
$cos{\text{ }}\theta {\text{ }} = {\text{ }}\dfrac{B}{H}$
$cos{\text{ }}\theta {\text{ }} = {\text{ }}\dfrac{5}{{13}}$
Similarly , calculating the value of $sin{\text{ }}\phi$

As ,
$cos{\text{ }}\phi = {\text{ }}\dfrac{{ - 3}}{5}$
As $\phi$ lies in third quadrant
We also know that ,
$cos{\text{ }}\phi {\text{ }} = \dfrac{B}{H}$
Comparing the two
Base $= {\text{ }}3$ and hypotenuse $= {\text{ }}5$

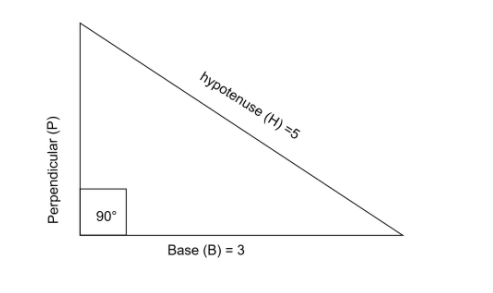
Using the formula of hypotenuse
${B^2} + {P^2} = {H^2}$
So ,
Value of $P = \sqrt {[{5^2} - {3^2}] }$
$P = \sqrt {[25 - 9] }$
$P = \sqrt {[16] }$
$P{\text{ }} = {\text{ }}4$
As the value of sin is negative in third quadrant , then
$sin{\text{ }}\phi {\text{ }} = {\text{ }}\dfrac{P}{H}$
$sin{\text{ }}\phi {\text{ }} = {\text{ }}\dfrac{{ - 4}}{5}$
Using the formula
$sin{\text{ }}\left( {{\text{ }}a{\text{ }} + {\text{ }}b{\text{ }}} \right){\text{ }} = {\text{ }}sin{\text{ }}a{\text{ }} \times {\text{ }}cos{\text{ }}b{\text{ }} + {\text{ }}sin{\text{ }}b{\text{ }} \times {\text{ }}cos{\text{ }}a$

Now putting the values in the formula , we get
$sin{\text{ }}\left( {{\text{ }}\theta {\text{ }} + {\text{ }}\phi } \right){\text{ }} = {\text{ }}sin{\text{ }}\theta {\text{ }} \times cos{\text{ }}\phi {\text{ }} + {\text{ }}sin{\text{ }}\phi {\text{ }} \times cos{\text{ }}\theta$
Substituting the values in the formula , we get
$sin{\text{ }}\left( {{\text{ }}\theta {\text{ }} + {\text{ }}\phi {\text{ }}} \right){\text{ }} = {\text{ }}\dfrac{{12}}{{13}}{\text{ }} \times {\text{ }}\left( {{\text{ }}\dfrac{{ - 3}}{5}} \right){\text{ }} + {\text{ }}\left( {{\text{ }}\dfrac{{ - 4}}{5}{\text{ }}} \right){\text{ }} \times {\text{ }}\dfrac{5}{{13}}$
$sin{\text{ }}\left( {{\text{ }}\theta {\text{ }} + {\text{ }}\phi {\text{ }}} \right){\text{ }} = {\text{ }}\dfrac{{ - 36}}{{65}}{\text{ }} - \dfrac{{20}}{{65}}$
$sin{\text{ }}\left( {{\text{ }}\theta {\text{ }} + {\text{ }}\phi {\text{ }}} \right){\text{ }} = {\text{ }}\dfrac{{ - 56}}{{65}}$
Hence , the value of $sin{\text{ }}\left( {{\text{ }}\theta {\text{ }} + {\text{ }}\phi {\text{ }}} \right){\text{ }} = {\text{ }}\dfrac{{ - 56}}{{65}}$
Thus , the correct option is $\left( 2 \right)$
So, the correct answer is “Option 2”.

Note : We have various trigonometric formulas used to solve the problem
The various trigonometric formulas used :
$sin{\text{ }}\left( {{\text{ }}a{\text{ }} + {\text{ }}b{\text{ }}} \right){\text{ }} = {\text{ }}sin{\text{ }}a{\text{ }} \times {\text{ }}cos{\text{ }}b{\text{ }} + {\text{ }}sin{\text{ }}b{\text{ }} \times {\text{ }}cos{\text{ }}a$
$sin{\text{ }}\left( {{\text{ }}a{\text{ }} - {\text{ }}b{\text{ }}} \right){\text{ }} = {\text{ }}sin{\text{ }}a{\text{ }} \times {\text{ }}cos{\text{ }}b{\text{ }} - {\text{ }}sin{\text{ }}b{\text{ }} \times {\text{ }}cos{\text{ }}a$
$cos{\text{ }}\left( {{\text{ }}a{\text{ }} + {\text{ }}b{\text{ }}} \right){\text{ }} = {\text{ }}cos{\text{ }}a{\text{ }} \times {\text{ }}cos{\text{ }}b{\text{ }} - {\text{ }}sin{\text{ }}b{\text{ }} \times {\text{ }}sin{\text{ }}a$
$cos{\text{ }}\left( {{\text{ }}a{\text{ }} - {\text{ }}b{\text{ }}} \right){\text{ }} = {\text{ }}cos{\text{ }}a{\text{ }} \times {\text{ }}cos{\text{ }}b{\text{ }} + {\text{ }}sin{\text{ }}b{\text{ }} \times {\text{ }}sin{\text{ }}a$
All the trigonometric functions are positive in first quadrant , the sin function are positive in second quadrant and rest are negative , the tan function are positive in third quadrant and rest are negative , the cos function are positive in fourth quadrant and rest are negative .