Question

If $\sin {\text{A = }}\dfrac{3}{4}$, calculate $\cos {\text{A}}$ and $\tan {\text{A}}$

Answer 1

We will draw a right angle triangle $\Delta {\text{ABC}}$ and assume that $\angle {\text{B}}$ is right angle. Now, we can find the length of hypotenuse, opposite side and adjacent side of the right angle triangle on the basis of information given to us in the question i.e. $\sin {\text{A = }}\dfrac{3}{4}$. We know that $\sin \theta = \dfrac{{{\text{opposite side}}}}{{{\text{Hypotenuse}}}}$.

Complete step-by-step solution:
The information given in the question is $\sin {\text{A = }}\dfrac{3}{4}$. Therefore, from this information we can find the length hypotenuse and opposite side of the right triangle because $\sin \theta = \dfrac{{{\text{opposite side}}}}{{{\text{hypotenuse}}}}$.

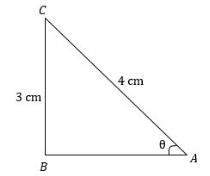
Therefore, ${\text{opposite side}} = 3{\text{cm}}$ and ${\text{hypotenuse}} = 4{\text{cm}}$.
Now, we know that $\cos \theta = \dfrac{{{\text{Adjacent side}}}}{{{\text{hypotenuse}}}}$. Therefore, in order to find $\cos {\text{A}}$we have to find the length of the adjacent side.
From the figure we can write that $\cos {\text{A = }}\dfrac{{{\text{Adjacent side}}}}{{{\text{Hypotenuse}}}} = \dfrac{{{\text{AB}}}}{{{\text{AC}}}}$. Therefore, here we have to find ${\text{AB}}$
From the figure we can write:
${\text{A}}{{\text{C}}^{\text{2}}}{\text{=A}}{{\text{B}}^{\text{2}}}{\text{+B}}{{\text{C}}^{\text{2}}} \\\ \Rightarrow {4^2} = {\text{A}}{{\text{B}}^{\text{2}}} + {3^2} \\\ \Rightarrow {\text{A}}{{\text{B}}^{\text{2}}} = {4^2} - {3^2} \\\ \Rightarrow {\text{A}}{{\text{B}}^{\text{2}}} = 16 - 9 = 7 \\\ \Rightarrow {\text{AB}} = \sqrt 7$
From the above calculation we get ${\text{AB}} = \sqrt 7 {\text{cm}}$, which is the base of the triangle $\Delta {\text{ABC}}$.
Therefore, $\cos {\text{A}} = \dfrac{{{\text{AB}}}}{{{\text{AC}}}} = \dfrac{{\sqrt 7 }}{4}$.
We know that $\tan \theta = \dfrac{{{\text{opposite side}}}}{{{\text{Adjacent side}}}}$. From the figure we can find the length of the opposite side and adjacent side. Therefore, from the figure we get ${\text{opposite side = BC}}$ and${\text{adjacent side = AB}}$.
Therefore, we can write$\tan {\text{A = }}\dfrac{{{\text{BC}}}}{{{\text{AB}}}}$.
Hence, $\tan {\text{A = }}\dfrac{{{\text{BC}}}}{{{\text{AB}}}} = \dfrac{3}{{\sqrt 7 }}$.

Therefore, the answer is $\cos {\text{A}} = \dfrac{{\sqrt 7 }}{4}$ and $\tan {\text{A = }}\dfrac{3}{{\sqrt 7 }}$.

Note: The important thing in this question is the diagram because if we don’t draw the diagram then we will not get the idea about what we require, to get the final answers of this question. The formulas of $\cos$ and $\tan$ are few important things that we need to recall while solving this question. In this question we also need to use the concept of Pythagoras theorem to find the remaining side of the right angle triangle.