Solveeit Logo
Login

Question

Question: If \(\sin \alpha = \dfrac{{ - 3}}{5}\), where \(\pi < \alpha < \dfrac{{3\pi }}{2}\) then, \(\dfrac{{...

If sin⁡α=−35\sin \alpha = \dfrac{{ - 3}}{5}, where π<α<3π2\pi < \alpha < \dfrac{{3\pi }}{2} then, cos⁡α2=\dfrac{{\cos \alpha }}{2} =
A. −110\dfrac{{ - 1}}{{\sqrt {10} }}
B. 110\dfrac{1}{{\sqrt {10} }}
C. 310\dfrac{3}{{\sqrt {10} }}
D. −310\dfrac{{ - 3}}{{\sqrt {10} }}

Explanation

Solution

The given problem has only the sin⁡\sin function and we are supposed to find the cos⁡\cos function. A range is also given, so we can first find out in which quadrant the function lies. For the given value of angle, we can find cos⁡\cos value. Then we move on to finding out the final answer.

Formula used:
cos⁡2A=2cos⁡2A−1\cos 2A = 2{\cos ^2}A - 1

Complete step by step answer:
The given expression is as follows,
sin⁡α=−35\sin \alpha = \dfrac{{ - 3}}{5}
We know that,
sin⁡α=oppositehypotenuse\sin \alpha = \dfrac{\text{opposite}}{\text{hypotenuse}}
We will consider the following right-angle triangle

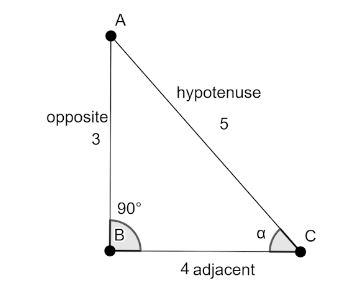
The range for the angle α\alpha is given as
π<α<3π2\pi < \alpha < \dfrac{{3\pi }}{2}
From the above, we can figure out that α\alpha lies in the Quadrant III. In Quadrant III both sin⁡\sin and the cos⁡\cos functions are negative.
We now, will find out the range of cos⁡α2\dfrac{{\cos \alpha }}{2}
The range is π<α<3π2\pi < \alpha < \dfrac{{3\pi }}{2}
To find out the range of α2\dfrac{\alpha }{2} divide the given range by two completely.
π2<α2<3π4\dfrac{\pi }{2} < \dfrac{\alpha }{2} < \dfrac{{3\pi }}{4}
This is the range of Quadrant II. The cos⁡\cos function is negative in the Quadrant II as well.
If, sin⁡α=−35\sin \alpha = \dfrac{{ - 3}}{5}
Then, using Pythagoras theorem, we have
cos⁡α=−45\cos \alpha = \dfrac{{ - 4}}{5}

Using the above-mentioned formulas,
cos⁡α=2cos⁡2(α2)−1\cos \alpha = 2{\cos ^2}\left( {\dfrac{\alpha }{2}} \right) - 1
We know the value of cos⁡α\cos \alpha
By substituting, we get
⇒−45=2cos⁡2(α2)\Rightarrow \dfrac{{ - 4}}{5} = 2{\cos ^2}\left( {\dfrac{\alpha }{2}} \right)
Rearranging the equation to get cos⁡(α2)\cos \left( {\dfrac{\alpha }{2}} \right) on the LHS,
⇒2cos⁡2(α2)=1−45⇒cos⁡2(α2)=110\Rightarrow 2{\cos ^2}\left( {\dfrac{\alpha }{2}} \right) = 1 - \dfrac{4}{5} \Rightarrow {\cos ^2}\left( {\dfrac{\alpha }{2}} \right) = \dfrac{1}{10}
Removing the square on both the sides, we get
cos⁡(α2)=110\cos \left( {\dfrac{\alpha }{2}} \right) = \sqrt {\dfrac{1}{{10}}}
Since α2\dfrac{\alpha }{2} lies in Quadrant II, the cos⁡\cos function will be negative.
Therefore, the final answer is cos⁡(α2)=−110\cos \left( {\dfrac{\alpha }{2}} \right) = \dfrac{{ - 1}}{{\sqrt {10} }}

Hence, option A is the correct answer.

Note: Noting down the quadrant and whether the function will be positive or negative is an important aspect. If the wrong sign is put, the final answer will be wrong. In the last step do not keep the root for the whole number because negative roots cannot be defined.