Question

If $\sin A=\dfrac{3}{4}$, calculate cos A and tan A
(a) $\cos A=\dfrac{\sqrt{3}}{4}\text{ and }\tan A=\dfrac{2}{5}$
(b) $\cos A=\dfrac{\sqrt{7}}{4}\text{ and }\tan A=\dfrac{3}{\sqrt{7}}$
(c) Both A and B
(d) None of these

Answer 1

Hint: Find the right-angled triangle which satisfies the value of the sine given in the question. Using the length of the sides of this triangle, find the values of cos and tan. These values of cos and tan are our required results.

Complete step-by-step answer:
We are given the value of sine of the angle in the question, it is written as
$\sin A=\dfrac{3}{4}$
Let us take a right-angled triangle ABC.

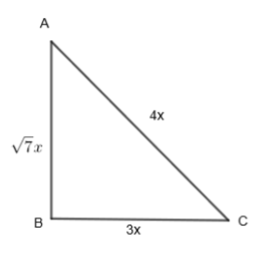
By properties of the triangle, we say the value of sin A to be:
$\sin A=\dfrac{\text{Opposite side to A}}{\text{Hypotenuse}}$
By substituting the values, we get the equation as follows:
$\dfrac{BC}{AC}=\dfrac{3}{4}$
From the equation, we can say the values of the sides to be:
BC = 3x….(i)
AC = 4x……(ii)
By applying Pythagoras theorem to ABC, we get the equation as:
${{\left( \text{Hypotenuse} \right)}^{2}}={{\left( \text{Height} \right)}^{2}}+{{\left( \text{Base} \right)}^{2}}$
By substituting the sides of the triangle ABC, we get it as:
${{\left( AC \right)}^{2}}={{\left( AB \right)}^{2}}+{{\left( BC \right)}^{2}}$
By substituting the known values, we get the equation as:
${{\left( 4x \right)}^{2}}={{\left( AB \right)}^{2}}+{{\left( 3x \right)}^{2}}$
By simplifying the above equation, we get its value as:
$16{{x}^{2}}=A{{B}^{2}}+9{{x}^{2}}$
By subtracting $9{{x}^{2}}$ on both the sides of the equation, we get it as:
$A{{B}^{2}}=7{{x}^{2}}$
By applying the square root on both the sides, we get it as
$AB=\sqrt{7{{x}^{2}}}$
By simplifying the expression, we get,
$AB=\sqrt{7}x$

By properties of the triangle, we have the relation as:
$\cos A=\dfrac{\text{Adjacent side to }\angle \text{A}}{\text{Hypotenuse}}$
$\tan A=\dfrac{\text{Opposite side}}{\text{Adjacent side}}$
By substituting in the above equation, we get cos value as
$\cos A=\dfrac{\sqrt{7}x}{4x}$
By canceling x, we get the value of cos A as
$\cos A=\dfrac{\sqrt{7}}{4}$
By substituting the value of tan, we get,
$\tan A=\dfrac{3x}{\sqrt{7}x}$
By canceling x, we get the value of tan to be
$\tan A=\dfrac{3}{\sqrt{7}}$
Therefore, these are the values of tan and cos.
Hence, option (b) is the right answer.

Note: Be careful while calculating the sides as if it is the main point of the whole solution. After getting the sides, don’t confuse between tan and cos as if you write them wrong, the whole result will be wrong. When you divide the sides, make it more simplified and you would get the final fraction as the result. Because the cos value is written as $\dfrac{1}{3}\text{ not }\dfrac{2}{6}$ though both are the same.