Solveeit Logo
Login

Question

Question: If \[\sin 2x = \dfrac{{2024}}{{2025}}\], where \[\dfrac{{5\pi }}{4} < x < \dfrac{{9\pi }}{4}\]. The ...

If sin⁡2x=20242025\sin 2x = \dfrac{{2024}}{{2025}}, where 5π4<x<9π4\dfrac{{5\pi }}{4} < x < \dfrac{{9\pi }}{4}. The value of sin⁡x−cos⁡x\sin x - \cos x is equal to?

Explanation

Solution

Here we use formula (a−b)2=a2+b2−2ab{(a - b)^2} = {a^2} + {b^2} - 2ab to open up the square of sin⁡x−cos⁡x\sin x - \cos x. Put the value of sin⁡2x\sin 2x in the expansion from the statement of the question and solve for the value using the trigonometric formulas. We check for the sign of the value obtained by converting sin⁡x−cos⁡x\sin x - \cos x into a sine function using the formula for sin⁡(A−B)\sin (A - B) and checking if it is positive or negative with the help of quadrant diagram.

  • sin⁡2x+cos⁡2x=1{\sin ^2}x + {\cos ^2}x = 1
  • 2sin⁡xcos⁡x=sin⁡2x2\sin x\cos x = \sin 2x
    *sin⁡(A−B)=sin⁡Acos⁡B−sin⁡Bcos⁡A\sin (A - B) = \sin A\cos B - \sin B\cos A

Complete step-by-step answer:
We are given sin⁡2x=20242025\sin 2x = \dfrac{{2024}}{{2025}}.
We have to find the value of sin⁡x−cos⁡x\sin x - \cos x.
We know (a−b)2=a2+b2−2ab{(a - b)^2} = {a^2} + {b^2} - 2ab.
Substitute the value of a=sin⁡x,b=cos⁡xa = \sin x,b = \cos x
⇒(sin⁡x−cos⁡x)2=sin⁡2x+cos⁡2x−2sin⁡xcos⁡x\Rightarrow {(\sin x - \cos x)^2} = {\sin ^2}x + {\cos ^2}x - 2\sin x\cos x
Use the trigonometric identity sin⁡2x+cos⁡2x=1{\sin ^2}x + {\cos ^2}x = 1 in the RHS of the equation.
⇒(sin⁡x−cos⁡x)2=1−2sin⁡xcos⁡x\Rightarrow {(\sin x - \cos x)^2} = 1 - 2\sin x\cos x
Now substitute the value of 2sin⁡xcos⁡x=sin⁡2x2\sin x\cos x = \sin 2x in the RHS of the equation.
⇒(sin⁡x−cos⁡x)2=1−sin⁡2x\Rightarrow {(\sin x - \cos x)^2} = 1 - \sin 2x
Substitute the value of sin⁡2x=20242025\sin 2x = \dfrac{{2024}}{{2025}} in the RHS of the equation.
⇒(sin⁡x−cos⁡x)2=1−20242025\Rightarrow {(\sin x - \cos x)^2} = 1 - \dfrac{{2024}}{{2025}}
Take LCM on the RHS of the equation.
⇒(sin⁡x−cos⁡x)2=2025−20242025\Rightarrow {(\sin x - \cos x)^2} = \dfrac{{2025 - 2024}}{{2025}}
⇒(sin⁡x−cos⁡x)2=12025\Rightarrow {(\sin x - \cos x)^2} = \dfrac{1}{{2025}}
We can write the value in the denominator as 2025=52×922025 = {5^2} \times {9^2}
On calculation we get 2025=(9×5)2=(45)22025 = {(9 \times 5)^2} = {(45)^2}
⇒(sin⁡x−cos⁡x)2=1(45)2\Rightarrow {(\sin x - \cos x)^2} = \dfrac{1}{{{{(45)}^2}}}
Take square root on both sides of the equation
⇒(sin⁡x−cos⁡x)2=1(45)2\Rightarrow \sqrt {{{(\sin x - \cos x)}^2}} = \sqrt {\dfrac{1}{{{{(45)}^2}}}}
Cancel square root by square power on both sides of the equation.
⇒sin⁡x−cos⁡x=±145\Rightarrow \sin x - \cos x = \pm \dfrac{1}{{45}}
We have to find the sign of sin⁡x−cos⁡x\sin x - \cos x
Let us multiply and divide the value sin⁡x−cos⁡x\sin x - \cos xby 2\sqrt 2 .
⇒22(sin⁡x−cos⁡x)=2(sin⁡x×12−cos⁡x×12)\Rightarrow \dfrac{{\sqrt 2 }}{{\sqrt 2 }}(\sin x - \cos x) = \sqrt 2 \left( {\sin x \times \dfrac{1}{{\sqrt 2 }} - \cos x \times \dfrac{1}{{\sqrt 2 }}} \right)
We substitute cos⁡π4=12\cos \dfrac{\pi }{4} = \dfrac{1}{{\sqrt 2 }} and sin⁡π4=12\sin \dfrac{\pi }{4} = \dfrac{1}{{\sqrt 2 }}
⇒22(sin⁡x−cos⁡x)=2(sin⁡x×cos⁡π4−cos⁡x×sin⁡π4)\Rightarrow \dfrac{{\sqrt 2 }}{{\sqrt 2 }}(\sin x - \cos x) = \sqrt 2 \left( {\sin x \times \cos \dfrac{\pi }{4} - \cos x \times \sin \dfrac{\pi }{4}} \right)
Use the formula sin⁡(A−B)=sin⁡Acos⁡B−sin⁡Bcos⁡A\sin (A - B) = \sin A\cos B - \sin B\cos A
⇒22(sin⁡x−cos⁡x)=2(sin⁡(x−π4))\Rightarrow \dfrac{{\sqrt 2 }}{{\sqrt 2 }}(\sin x - \cos x) = \sqrt 2 \left( {\sin (x - \dfrac{\pi }{4})} \right)
Now we are given the condition 5π4<x<9π4\dfrac{{5\pi }}{4} < x < \dfrac{{9\pi }}{4}
Therefore subtract π4\dfrac{\pi }{4} from all values in the inequality 5π4<x<9π4\dfrac{{5\pi }}{4} < x < \dfrac{{9\pi }}{4}
⇒5π4−π4<x−π4<9π4−π4\Rightarrow \dfrac{{5\pi }}{4} - \dfrac{\pi }{4} < x - \dfrac{\pi }{4} < \dfrac{{9\pi }}{4} - \dfrac{\pi }{4}
⇒4π4<x−π4<8π4\Rightarrow \dfrac{{4\pi }}{4} < x - \dfrac{\pi }{4} < \dfrac{{8\pi }}{4}
Cancel the same terms from numerator and denominator.
⇒π<x−π4<2π\Rightarrow \pi < x - \dfrac{\pi }{4} < 2\pi
Now apply sine function to values in the inequality
⇒sin⁡π<sin⁡(x−π4)<sin⁡2π\Rightarrow \sin \pi < \sin (x - \dfrac{\pi }{4}) < \sin 2\pi
We see the quadrant diagram to check if sine is positive or negative in between π\pi and 2π2\pi

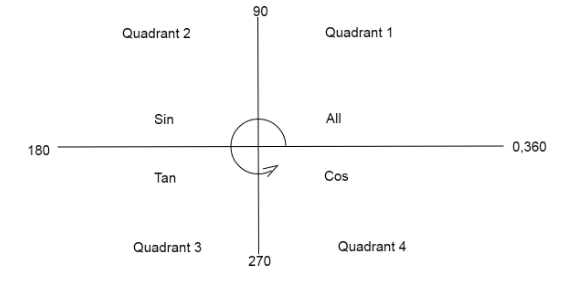
Since, sine function is negative between π(180∘)\pi ({180^ \circ })and 2π(360∘)2\pi ({360^ \circ })
⇒22(sin⁡x−cos⁡x)=2(sin⁡(x−π4))\Rightarrow \dfrac{{\sqrt 2 }}{{\sqrt 2 }}(\sin x - \cos x) = \sqrt 2 \left( {\sin (x - \dfrac{\pi }{4})} \right) is a negative value.

Therefore, value of sin⁡x−cos⁡x=−145\sin x - \cos x = - \dfrac{1}{{45}}

Note: Students make mistake of writing the answer after removing the square root as 145\dfrac{1}{{45}}, which is wrong because we have to take both the possibilities of negative and positive terms after removing square root from any value.
Also, keep in mind while checking the values from the quadrant diagram we move in an anticlockwise direction.