Question
Question: If $\sin^{-1}(\sin\frac{7}{2}) + \cos^{-1}(\cos\frac{9}{2}) + \tan^{-1}(\tan\frac{11}{2}) + \cot^{-1...
If sin−1(sin27)+cos−1(cos29)+tan−1(tan211)+cot−1(cot213)=aπ+b, then (a+b) equals
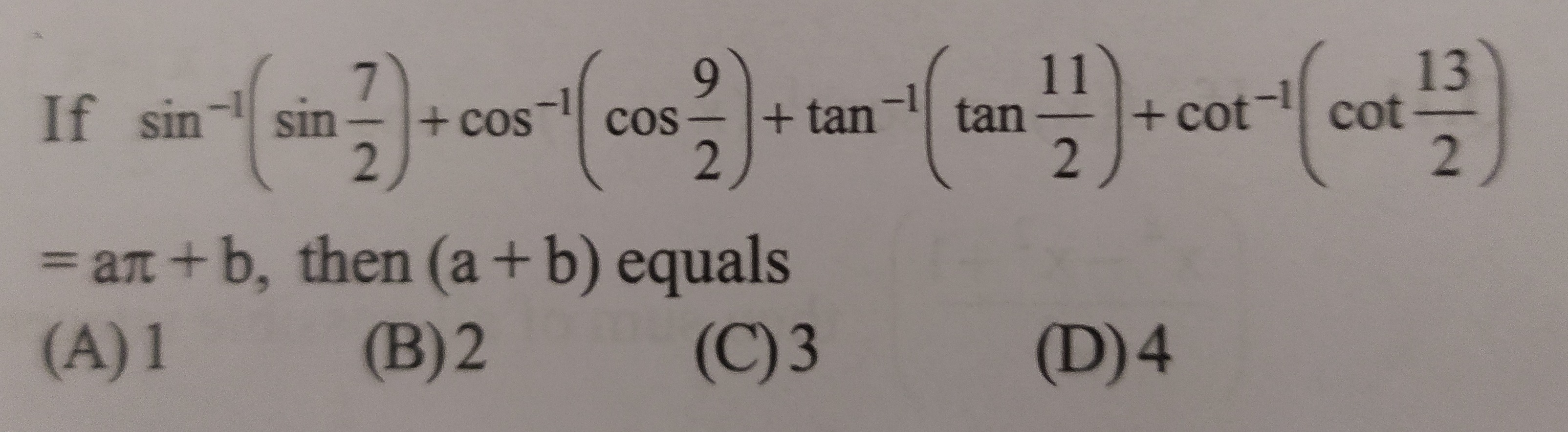
1
2
3
4
3
Solution
Let E=sin−1(sin27)+cos−1(cos29)+tan−1(tan211)+cot−1(cot213).
We need to evaluate each term using the properties of inverse trigonometric functions.
The relevant properties are:
sin−1(sinx)=x if x∈[−2π,2π]
cos−1(cosx)=x if x∈[0,π]
tan−1(tanx)=x if x∈(−2π,2π)
cot−1(cotx)=x if x∈(0,π)
We use the approximation π≈3.1416. 2π≈1.5708, π≈3.1416, 23π≈4.7124, 2π≈6.2832.
Term 1: sin−1(sin27)
27=3.5. The range of sin−1(sinx) is [−2π,2π].
Since 2π<27<23π (i.e., 1.5708<3.5<4.7124), we use the formula sin−1(sinx)=π−x.
So, sin−1(sin27)=π−27.
Check if π−27∈[−2π,2π].
π−27≈3.1416−3.5=−0.3584.
Since −1.5708≤−0.3584≤1.5708, this is correct.
Term 2: cos−1(cos29)
29=4.5. The range of cos−1(cosx) is [0,π].
Since π<29<2π (i.e., 3.1416<4.5<6.2832), we use the formula cos−1(cosx)=2π−x.
So, cos−1(cos29)=2π−29.
Check if 2π−29∈[0,π].
2π−29≈6.2832−4.5=1.7832.
Since 0≤1.7832≤3.1416, this is correct.
Term 3: tan−1(tan211)
211=5.5. The range of tan−1(tanx) is (−2π,2π).
Since 23π<211<25π (i.e., 4.7124<5.5<7.8540), we need to subtract 2π from 211.
211−2π.
Check if 211−2π∈(−2π,2π).
211−2π≈5.5−6.2832=−0.7832.
Since −1.5708<−0.7832<1.5708, this is correct.
So, tan−1(tan211)=211−2π.
Term 4: cot−1(cot213)
213=6.5. The range of cot−1(cotx) is (0,π).
Since 2π<213<3π (i.e., 6.2832<6.5<9.4248), we need to subtract 2π from 213.
213−2π.
Check if 213−2π∈(0,π).
213−2π≈6.5−6.2832=0.2168.
Since 0<0.2168<3.1416, this is correct.
So, cot−1(cot213)=213−2π.
Now, sum the terms:
E=(π−27)+(2π−29)+(211−2π)+(213−2π)
E=(π+2π−2π−2π)+(−27−29+211+213)
E=(3π−4π)+(2−7−9+11+13)
E=−π+(2−16+24)
E=−π+28
E=−π+4
E=4−π
The given form is aπ+b.
Comparing 4−π with aπ+b, we get a=−1 and b=4.
We need to find (a+b).
a+b=−1+4=3.
