Question
Question: If $\sin^{-1}(\sin 4) + \cos^{-1}(\cos 8) + \tan^{-1}(\tan 6) + \cot^{-1}(\cot 10) = a + b\pi$ then ...
If sin−1(sin4)+cos−1(cos8)+tan−1(tan6)+cot−1(cot10)=a+bπ then (a + b) equals
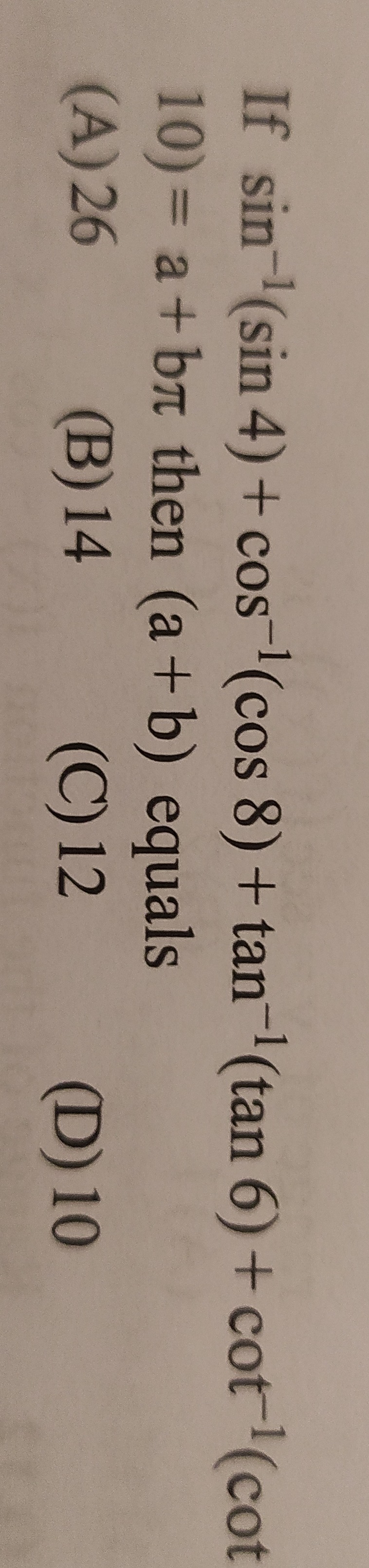
26
14
12
10
14
Solution
The problem requires evaluating the sum of inverse trigonometric functions with arguments outside their principal ranges. We will use the properties of inverse trigonometric functions to find the equivalent values within the principal ranges. The principal ranges are:
sin−1x∈[−2π,2π]
cos−1x∈[0,π]
tan−1x∈(−2π,2π)
cot−1x∈(0,π)
We use the approximation π≈3.1416.
π/2≈1.5708
π≈3.1416
3π/2≈4.7124
2π≈6.2832
5π/2≈7.8540
3π≈9.4248
7π/2≈10.9956
- sin−1(sin4):
The argument is 4. The principal range for sin−1 is [−π/2,π/2].
Since π<4<3π/2 (i.e., 3.1416<4<4.7124), we use the property sin−1(sinx)=π−x for x∈[π/2,3π/2].
So, sin−1(sin4)=π−4.
Check if π−4 is in [−π/2,π/2]: π−4≈3.1416−4=−0.8584.
Since −1.5708≤−0.8584≤1.5708, the value is correct.
- cos−1(cos8):
The argument is 8. The principal range for cos−1 is [0,π].
Since 2π<8<3π (i.e., 6.2832<8<9.4248), we use the property cos−1(cosx)=x−2π for x∈[2π,3π].
So, cos−1(cos8)=8−2π.
Check if 8−2π is in [0,π]: 8−2π≈8−6.2832=1.7168.
Since 0≤1.7168≤3.1416, the value is correct.
- tan−1(tan6):
The argument is 6. The principal range for tan−1 is (−π/2,π/2).
Since 3π/2<6<2π (i.e., 4.7124<6<6.2832), we use the property tan−1(tanx)=x−2π for x∈(3π/2,5π/2).
So, tan−1(tan6)=6−2π.
Check if 6−2π is in (−π/2,π/2): 6−2π≈6−6.2832=−0.2832.
Since −1.5708<−0.2832<1.5708, the value is correct.
- cot−1(cot10):
The argument is 10. The principal range for cot−1 is (0,π).
Since 3π<10<7π/2 (i.e., 9.4248<10<10.9956), we use the property cot−1(cotx)=x−3π for x∈(3π,4π).
So, cot−1(cot10)=10−3π.
Check if 10−3π is in (0,π): 10−3π≈10−9.4248=0.5752.
Since 0<0.5752<3.1416, the value is correct.
Now, sum the terms:
sin−1(sin4)+cos−1(cos8)+tan−1(tan6)+cot−1(cot10)=(π−4)+(8−2π)+(6−2π)+(10−3π)
=(π−2π−2π−3π)+(−4+8+6+10)
=(1−2−2−3)π+(−4+8+6+10)
=−6π+(4+16)
=−6π+20
=20−6π
We are given that the sum equals a+bπ.
Comparing 20−6π with a+bπ, we have a=20 and b=−6.
We need to find the value of a+b.
a+b=20+(−6)=20−6=14.
The final answer is 14.
Explanation of the solution:
- Evaluate each term sin−1(sin4), cos−1(cos8), tan−1(tan6), cot−1(cot10) by finding the equivalent angle within the principal range of the respective inverse trigonometric function.
- For sin−1(sin4), since π<4<3π/2, sin−1(sin4)=π−4.
- For cos−1(cos8), since 2π<8<3π, cos−1(cos8)=8−2π.
- For tan−1(tan6), since 3π/2<6<2π, tan−1(tan6)=6−2π.
- For cot−1(cot10), since 3π<10<4π, cot−1(cot10)=10−3π.
- Sum the evaluated terms: (π−4)+(8−2π)+(6−2π)+(10−3π)=(1−2−2−3)π+(−4+8+6+10)=−6π+20=20−6π.
- Compare the result with a+bπ to find a=20 and b=−6.
- Calculate a+b=20+(−6)=14.
The final answer is 14.
