Question
Question: If $\sin^{-1}\left(\frac{x}{\sqrt{x^2+5^2}}\right)=\tan^{-1}\left(\frac{x}{k}\right)$, then $k$ is e...
If sin−1(x2+52x)=tan−1(kx), then k is equal to
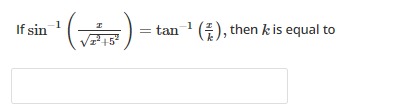
5
Solution
To solve the given equation sin−1(x2+52x)=tan−1(kx), we need to convert the left-hand side into a tan−1 form.
Let θ=sin−1(x2+52x). This implies sinθ=x2+52x. The range of θ is [−2π,2π].
We can find cosθ using the identity cos2θ=1−sin2θ. cos2θ=1−(x2+52x)2 cos2θ=1−x2+52x2 cos2θ=x2+52x2+52−x2 cos2θ=x2+5252 Taking the square root, cosθ=±x2+525. Since θ∈[−2π,2π], cosθ must be non-negative. Therefore, cosθ=x2+525.
Now we can find tanθ: tanθ=cosθsinθ=x2+525x2+52x=5x.
So, θ=tan−1(5x). Note that θ cannot be ±2π because sinθ=±1 would imply x=±x2+52, which leads to x2=x2+25, i.e., 0=25, which is impossible. Thus, θ∈(−2π,2π), which is the principal range of tan−1.
Substituting this back into the original equation: tan−1(5x)=tan−1(kx).
For this equality to hold true for all valid x, the arguments of the tan−1 functions must be equal: 5x=kx.
Assuming x=0, we can cancel x from both sides: 51=k1 k=5.
If x=0, the equation becomes sin−1(0)=tan−1(0), which is 0=0. This holds for any non-zero k. However, the question asks for "k is equal to", implying a unique value that satisfies the equality for all relevant x. Thus, k=5 is the unique value.
