Solveeit Logo
Login

Question

Question: If \({\sin ^{ - 1}}{\text{x = y}}\), then A. \(0 \leqslant {\text{y}} \leqslant \pi \) B. \( - \...

If sin⁡−1x = y{\sin ^{ - 1}}{\text{x = y}}, then
A. 0⩽y⩽π0 \leqslant {\text{y}} \leqslant \pi
B. −π2⩽y⩽π2 - \dfrac{\pi }{2} \leqslant {\text{y}} \leqslant \dfrac{\pi }{2}
C. 0<y < π0 < {\text{y < }}\pi
D. −π2<y < π2 - \dfrac{\pi }{2} < {\text{y < }}\dfrac{\pi }{2}

Explanation

Solution

Hint: To solve this question we will write sin⁡−1x = y{\sin ^{ - 1}}{\text{x = y}}as x = siny{\text{x = siny}}and then draw the graph of siny and find the minimum and maximum value of siny and we will find the interval in which y lies.

Complete step by step answer:
Now, we have sin⁡−1x = y{\sin ^{ - 1}}{\text{x = y}}which can be written as
x = siny{\text{x = siny}}
Now,
At 0, sin y = 0, at π2\dfrac{\pi }{2}, sin y = 0, at π\pi , sin y = 0. Also, at −π2 - \dfrac{\pi }{2}, sin y = -1
So, we will draw the graph of siny according to the above values.
Hint: To solve this question we will write sin⁡−1x = y{\sin ^{ - 1}}{\text{x = y}}as x = siny{\text{x = siny}}and then draw the graph of siny and find the minimum and maximum value of siny and we will find the interval in which y lies.
Now, we have sin⁡−1x = y{\sin ^{ - 1}}{\text{x = y}}which can be written as
x = siny{\text{x = siny}}
Now,
At 0, sin y = 0, at π2\dfrac{\pi }{2}, sin y = 0, at π\pi , sin y = 0. Also, at −π2 - \dfrac{\pi }{2}, sin y = -1
So, we will draw the graph of siny according to the above values.

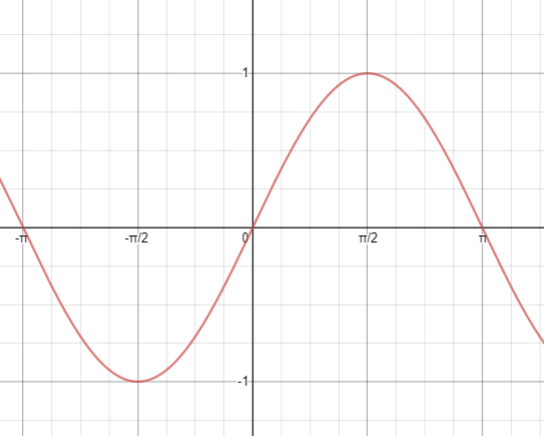
Now, from the graph of x = siny{\text{x = siny}}, we know that the maximum value of x is 1 and minimum value is -1, i.e.
−1⩽x⩽1- 1 \leqslant {\text{x}} \leqslant {\text{1}}
As, x = siny{\text{x = siny}}, we get
−1⩽sin⁡y⩽1- 1 \leqslant \sin {\text{y}} \leqslant {\text{1}}
Taking the inverse trigonometric function sin⁡−1{\sin ^{ - 1}} in the above equation, we get
sin⁡−1(−1)⩽sin⁡−1(sin⁡y)⩽sin−1(1){\sin ^{ - 1}}( - 1) \leqslant {\sin ^{ - 1}}(\sin {\text{y)}} \leqslant {\text{si}}{{\text{n}}^{ - 1}}(1)
As, sin⁡−1(−1) = - π2{\sin ^{ - 1}}( - 1){\text{ = - }}\dfrac{\pi }{2} and sin⁡−1(1) = π2{\sin ^{ - 1}}(1){\text{ = }}\dfrac{\pi }{2}. Also, sin⁡−1(sin⁡x) = x{\sin ^{ - 1}}(\sin {\text{x) = x}}
Therefore, we get
−π2⩽y⩽π2- \dfrac{\pi }{2} \leqslant {\text{y}} \leqslant \dfrac{\pi }{2}
So, option (B) is correct.

Note: When we come up with such types of questions, we will rewrite the given function and remove all inverse functions from the expression. Then we will draw the graph of the expression formed. With the help of the graph drawn, we will find the interval of the function. The interval has extremum values between which the curve of the function oscillates for example the curve of sinx oscillates between -1 and 1 and has a minimum value of -1 and maximum value of 1.