Question
Question: If \[\sec \theta = \dfrac{5}{4}\], show that \[\left( {\dfrac{{\sin \theta - 2\cos \theta }}{{\tan \...
If secθ=45, show that (tanθ−cosθsinθ−2cosθ)=712?
Solution
In order to solve this question we have given a trigonometry relation and from that function, we are going to use the relation of sides of a right-angle triangle and then find perpendicular by using Pythagoras theorem. Then find all the required relations and put them on the left-hand side of the proof equation and solve that to get the final answer.
Complete step by step answer:
We have given the value of a trigonometric function secθ=45. We have to prove (tanθ−cosθsinθ−2cosθ)=712.
On the left hand side of the equation.
⇒(tanθ−cosθsinθ−2cosθ)
To solve this side we must know all the values of the trigonometric function. So, now we are going to find all the values.
secθ=45..........(given)
On writing the sec trigonometric function in terms of sides of a right-angle triangle.
Right angle triangle is as shown in the figure.
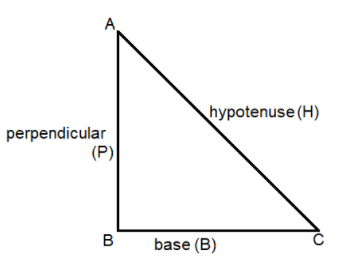
BH=712
From this relation we use Pythagoras theorem and find the value of perpendicular.
P2+B2=H2
On rearranging this theorem.
P=H2−B2
On putting the value of base and hypotenuse.
P=25−16
On further calculating
P=3
Now we are going to find all the required values that are used in the left side of the proof part.
sinθ=53
⇒cosθ=54
⇒tanθ=43
⇒(tanθ−cosθsinθ−2cosθ)
On putting all these values in the left side of the proof part.
⇒43−5453−254
On calculating some of this equation.
⇒2015−1653−8
On further simplifying this equation.
⇒2015−1653−8
On further solving
⇒(5−5×−120)
Negative is canceled by negative and 5 is canceled because this is a common factor.
⇒20
Hence, the left-hand side is not equal to the right-hand side.
So the proved relation is wrong.
Note: In order to solve this question, students must have a knowledge of all the trigonometric relations in terms of sides of the right-angle triangle and theorems related to the triangle. There is another way to solve this question that is changing all the trigonometric functions in only one but there is a higher probability of committing mistakes.
