Solveeit Logo
Login

Question

Question: if \(\sec \theta =2p\) and \(\tan \theta =\dfrac{2}{p}\), then the value of \(2\left( {{p}^{2}}-\dfr...

if sec⁡θ=2p\sec \theta =2p and tan⁡θ=2p\tan \theta =\dfrac{2}{p}, then the value of 2(p2−1p2)2\left( {{p}^{2}}-\dfrac{1}{{{p}^{2}}} \right) is
[a] 12\dfrac{1}{2}
[b] 12\dfrac{1}{\sqrt{2}}
[c] 14\dfrac{1}{4}
[d] 18\dfrac{1}{8}

Explanation

Solution

Hint: Form a triangle which satisfies tan⁡θ=2p\tan \theta =\dfrac{2}{p}. Now using this find the value for sec⁡θ\sec \theta . Hence form an equation in p and hence find the value of 2(p2−1p2)2\left( {{p}^{2}}-\dfrac{1}{{{p}^{2}}} \right). Alternatively, use sec⁡2x−tan⁡2x=1{{\sec }^{2}}x-{{\tan }^{2}}x=1.

Complete step-by-step answer:
Trigonometric ratios:
There are six trigonometric ratios defined on an angle of a right-angled triangle, viz sine, cosine,
tangent, cotangent, secant and cosecant.
The sine of an angle is defined as the ratio of the opposite side to the hypotenuse.
The cosine of an angle is defined as the ratio of the adjacent side to the hypotenuse.
The tangent of an angle is defined as the ratio of the opposite side to the adjacent side.
The cotangent of an angle is defined as the ratio of the adjacent side to the opposite side.
The secant of an angle is defined as the ratio of the hypotenuse to the adjacent side.
The cosecant of an angle is defined as the ratio of the hypotenuse to the adjacent side.
Observe that sine and cosecant are multiplicative inverses of each other, cosine and secant are
multiplicative inverses of each other, and tangent and cotangent are multiplicative inverses of each
other.
We have sin⁡2x+cos⁡2x=1,sec⁡2x=1+tan⁡2x{{\sin }^{2}}x+{{\cos }^{2}}x=1,{{\sec }^{2}}x=1+{{\tan }^{2}}x and csc⁡2x=1+cot⁡2x{{\csc }^{2}}x=1+{{\cot }^{2}}x. These identities are called Pythagorean identities.

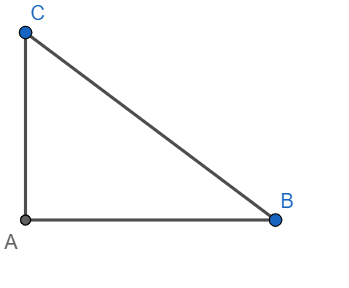
Let AC = 2 and AB = p
Using Pythagoras theorem, we have
BC2=AB2+AC2 ⇒BC2=22+p2=4+p2 \begin{aligned} & \text{B}{{\text{C}}^{2}}=\text{A}{{\text{B}}^{2}}\text{+A}{{\text{C}}^{2}} \\\ & \Rightarrow \text{B}{{\text{C}}^{2}}={{2}^{2}}+{{p}^{2}}=4+{{p}^{2}} \\\ \end{aligned}
Now we have
sec⁡θ=2p ⇒sec⁡2θ=4p2 \begin{aligned} & \sec \theta =2p \\\ & \Rightarrow {{\sec }^{2}}\theta =4{{p}^{2}} \\\ \end{aligned}
We know that the secant of an angle is the ratio of the hypotenuse to the adjacent side.
Hence sec⁡2θ=(BCAB)2=4+p2p2=4p2+1{{\sec }^{2}}\theta ={{\left( \dfrac{\text{BC}}{\text{AB}} \right)}^{2}}=\dfrac{4+{{p}^{2}}}{{{p}^{2}}}=\dfrac{4}{{{p}^{2}}}+1
Hence, we have
4p2+1=4p2 ⇒4p2−4p2=1 ⇒4(p2−1p2)=1 \begin{aligned} & \dfrac{4}{{{p}^{2}}}+1=4{{p}^{2}} \\\ & \Rightarrow 4{{p}^{2}}-\dfrac{4}{{{p}^{2}}}=1 \\\ & \Rightarrow 4\left( {{p}^{2}}-\dfrac{1}{{{p}^{2}}} \right)=1 \\\ \end{aligned}
Hence, we have 2(p2−1p2)=122\left( {{p}^{2}}-\dfrac{1}{{{p}^{2}}} \right)=\dfrac{1}{2}
Hence option [a] is correct.

Note: Alternative Method: Best Method.
We have sec⁡θ+tan⁡θ=2p+2p\sec \theta +\tan \theta =2p+\dfrac{2}{p}
and sec⁡θ−tan⁡θ=2p−2p\sec \theta -\tan \theta =2p-\dfrac{2}{p}
Multiplying, we get
(sec⁡θ−tan⁡θ)(sec⁡θ+tan⁡θ)=(2p+2p)(2p−2p) ⇒sec⁡2θ−tan⁡2θ=4p2−4p2 ⇒4p2−4p2=1 ⇒2(p2−1p2)=12 \begin{aligned} & \left( \sec \theta -\tan \theta \right)\left( \sec \theta +\tan \theta \right)=\left( 2p+\dfrac{2}{p} \right)\left( 2p-\dfrac{2}{p} \right) \\\ & \Rightarrow {{\sec }^{2}}\theta -{{\tan }^{2}}\theta =4{{p}^{2}}-\dfrac{4}{{{p}^{2}}} \\\ & \Rightarrow 4{{p}^{2}}-\dfrac{4}{{{p}^{2}}}=1 \\\ & \Rightarrow 2\left( {{p}^{2}}-\dfrac{1}{{{p}^{2}}} \right)=\dfrac{1}{2} \\\ \end{aligned}
Hence option [a] is correct.