Question

If $\sec A=\dfrac{5}{4}$, verify that
$\dfrac{3\sin A-4{{\sin }^{3}}A}{4{{\cos }^{3}}A-3\cos A}=\dfrac{3\tan A-{{\tan }^{3}}A}{1-3{{\tan }^{2}}A}$

Answer 1

Hint:First of all, consider a triangle ABC, right-angled at B. Now use $\sec A=\dfrac{Hypotenuse}{Base}=\dfrac{5}{4}$ and let hypotenuse and base be 5x and 4x respectively. Now, find the remaining side by using the Pythagoras theorem. Now find, $\sin A=\dfrac{P}{H},\cos A=\dfrac{B}{H}$ and $\tan A=\dfrac{P}{B}$ and substitute in the given equation to prove that LHS = RHS.

Complete step-by-step answer:
Here, we are given that $\sec A=\dfrac{5}{4}$. We have to verify that $\dfrac{3\sin A-4{{\sin }^{3}}A}{4{{\cos }^{3}}A-3\cos A}=\dfrac{3\tan A-{{\tan }^{3}}A}{1-3{{\tan }^{2}}A}$.
We are given that,
$\sec A=\dfrac{5}{4}....\left( i \right)$
We know that,
$\sec A=\dfrac{Hypotenuse}{Base}....\left( ii \right)$
From equation (i) and (ii), we get,
$\dfrac{5}{4}=\dfrac{Hypotenuse}{Base}$
Let us consider a triangle ABC, right-angled at B.

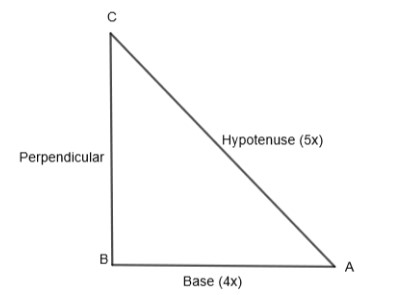
Let base AB be equal to 4x and hypotenuse be equal to 5x.
We know that Pythagoras theorem states that in a right-angled triangle, the square of the hypotenuse side is equal to the sum of the squares of the other two sides. So, in the above triangle ABC, by applying Pythagoras theorem, we get,
${{\left( AB \right)}^{2}}+{{\left( BC \right)}^{2}}={{\left( AC \right)}^{2}}$
Now by substituting the value of AB = 4x and AC = 5x, we get,
${{\left( 4x \right)}^{2}}+{{\left( BC \right)}^{2}}={{\left( 5x \right)}^{2}}$
$16{{x}^{2}}+{{\left( BC \right)}^{2}}=25{{x}^{2}}$
$B{{C}^{2}}=25{{x}^{2}}-16{{x}^{2}}$
$B{{C}^{2}}=9{{x}^{2}}$
$BC=\sqrt{9{{x}^{2}}}=3x$
Now, we know that,
$\sin A=\dfrac{Perpendicular}{Hypotenuse}$
$\cos A=\dfrac{Base}{Hypotenuse}$
$\tan A=\dfrac{Perpendicular}{Base}$
We can see that with respect to angle A,
Perpendicular = BC = 3x
Base = AB = 4x
Hypotenuse = AC = 5x
So, we get,
$\sin A=\dfrac{BC}{AC}=\dfrac{3x}{5x}=\dfrac{3}{5}$
$\cos A=\dfrac{AB}{AC}=\dfrac{4x}{5x}=\dfrac{4}{5}$
$\tan A=\dfrac{BC}{AB}=\dfrac{3x}{4x}=\dfrac{3}{4}$
Now, let us consider the equation given in the question,
$\dfrac{3\sin A-4{{\sin }^{3}}A}{4{{\cos }^{3}}A-3\cos A}=\dfrac{3\tan A-{{\tan }^{3}}A}{1-3{{\tan }^{2}}A}$
By substituting the value of sin A, cos A and tan A, we get,
$\dfrac{3\left( \dfrac{3}{5} \right)-4{{\left( \dfrac{3}{5} \right)}^{3}}}{4{{\left( \dfrac{4}{5} \right)}^{3}}-3\left( \dfrac{4}{5} \right)}=\dfrac{3\left( \dfrac{3}{4} \right)-{{\left( \dfrac{3}{4} \right)}^{3}}}{1-3{{\left( \dfrac{3}{4} \right)}^{2}}}$
$\dfrac{\dfrac{9}{5}-4\left( \dfrac{27}{125} \right)}{4\left( \dfrac{64}{125} \right)-\dfrac{12}{5}}=\dfrac{\dfrac{9}{4}-\left( \dfrac{27}{64} \right)}{1-3\left( \dfrac{9}{16} \right)}$
$\dfrac{\dfrac{\left( 25\times 9 \right)-\left( 27\times 4 \right)}{125}}{\dfrac{\left( 4\times 64 \right)-\left( 12\times 25 \right)}{125}}=\dfrac{\dfrac{\left( 16\times 9 \right)-27}{64}}{\dfrac{16-27}{16}}$
$\dfrac{225-108}{256-300}=\left( \dfrac{144-27}{64} \right)\times \left( \dfrac{16}{-11} \right)$
$\dfrac{117}{-44}=\dfrac{117}{4\times \left( -11 \right)}$
$\dfrac{117}{-44}=\dfrac{117}{-44}$
Hence, LHS = RHS
Therefore, we have verified that
$\dfrac{3\sin A-4{{\sin }^{3}}A}{4{{\cos }^{3}}A-3\cos A}=\dfrac{3\tan A-{{\tan }^{3}}A}{1-3{{\tan }^{2}}A}$

Note: In this question, students can also find cos A by using $\cos A=\dfrac{1}{\sec A}$, tan A by using $1+{{\tan }^{2}}A={{\sec }^{2}}A$ and sin A by using $\dfrac{\sin A}{\cos A}=\tan A$ and then substitute these values in the given equation to verify it. Also, students must keep in mind that when nothing is given about the angle, we consider it to be in the first quadrant. So, all the trigonometric ratios would be positive.