Question
Question: If $S_n = \sum_{r=1}^{n} r!$ then for $n > 6$ then $\sin^{-1} \left( \sin \left(S_n -7 \left[ \frac{...
If Sn=∑r=1nr! then for n>6 then sin−1(sin(Sn−7[7Sn])) is:
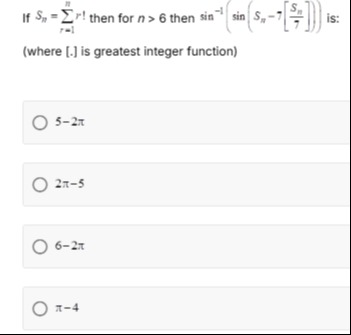
5 - 2\pi
2\pi - 5
6 - 2\pi
\pi - 4
5 - 2\pi
Solution
The expression Sn−7[7Sn] represents the remainder when Sn is divided by 7. For n>6, any term r! where r≥7 is divisible by 7, meaning r!≡0(mod7). Therefore, for n>6, Sn≡1!+2!+3!+4!+5!+6!(mod7).
Calculating the values modulo 7: 1!≡1(mod7) 2!≡2(mod7) 3!≡6(mod7) 4!=24≡3(mod7) 5!=120≡1(mod7) 6!=720≡6(mod7)
Summing these remainders: Sn≡1+2+6+3+1+6=19≡5(mod7). So, the expression simplifies to sin−1(sin(5)).
The principal value range for sin−1(x) is [−2π,2π]. We need to find a value y such that sin(y)=sin(5) and y∈[−2π,2π]. We know that sin(x)=sin(x−2kπ) for any integer k. Let k=1, then we consider 5−2π. Approximating π≈3.14159, we get 2π≈6.28318. So, 5−2π≈5−6.28318=−1.28318. The range [−2π,2π] is approximately [−1.5708,1.5708]. Since −1.5708<−1.28318<1.5708, the value 5−2π lies within the principal range. Therefore, sin−1(sin(5))=5−2π.
