Question

If ${S_1}$ and ${S_2}$ are two hollow spheres enclosing charges $q$ and $2q$ respectively then what is the ratio of electric flux through ${S_1}$ and ${S_2}$? How will the electric flux through ${S_1}$ change if a medium of di-electric constant $5$ is introduced inside ${S_1}$.

Answer 1

we will first calculate the electric flux by using the Gauss’ law. After this, we will find the ratio of the electric flux by dividing both the electric flux. Now, the change in the electric flux can be calculated by using the potential difference formula.

Formula used:
The formula of potential difference is given by
$V = Ed$
Here, $V$ is the potential difference, $E$ is the electric field and $d$ is the distance between the plates.

Complete step by step answer:
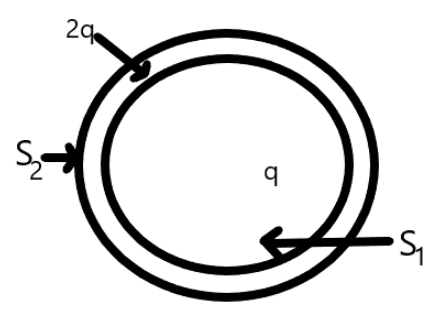
Consider two hollow spheres ${S_1}$ and ${S_2}$ that will enclose charges $q$ and $2q$ respectively as shown below;

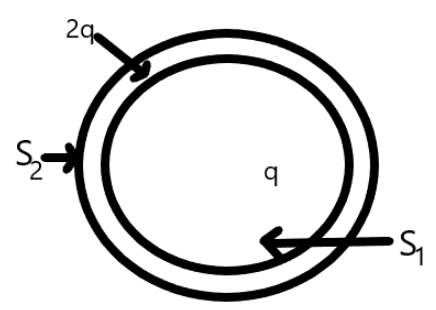
Now, let the electric flux enclosed by the sphere ${S_1}$ is ${\phi _1}$ and the electric flux enclosed by the sphere ${S_2}$ is ${\phi _2}$.Now, from the Gauss’ law, the electric flux is given by,
$\phi = \dfrac{q}{{{\varepsilon _0}}}$
Therefore, the electric flux in the sphere ${S_1}$ is given by
${\phi _1} = \dfrac{q}{{{\varepsilon _0}}}$
Also, the electric flux in the sphere ${S_2}$ is given by
${\phi _2} = \dfrac{{3q}}{{{\varepsilon _0}}}$
Now, the ratio of the electric flux is given below
$\dfrac{{{\phi _1}}}{{{\phi _2}}} = \dfrac{1}{3}$
Now, according to coulomb’s law of charges, the potential difference between the charges is given by
$V = Ed$
Here, $E$ is the electric field in the sphere and is given by
$E = \dfrac{q}{{A{\varepsilon _0}}}$
Therefore, the value of potential difference is given by
$V = \dfrac{q}{{A{\varepsilon _0}}}d$
$\Rightarrow \,V = \phi \dfrac{d}{A}$
$\therefore \,\phi = \dfrac{{AV}}{d}$
Therefore, from the above equation, we can say that the flux $\phi$ in the sphere will be inversely proportional to distance $d$.Now, if the di-electric of $5$ is introduced inside the sphere ${S_1}$ , the distance $d$ will increase by $5$ times and therefore, the electric flux will increase by $\dfrac{1}{5}$ times.

Note: Now, you might get confused about how the charge of the sphere ${S_2}$ is $3q$. This is because the sphere ${S_2}$ contains the sphere ${S_1}$, therefore, the charge will add up. Also, we have used the concept of capacitors that contains two capacitors.