Question
Question: If roots of the equation $4K^2-4K-3 = 0$ are slope of tangents drawn from a point $P$ on the parabol...
If roots of the equation 4K2−4K−3=0 are slope of tangents drawn from a point P on the parabola y2=12x and let tangents touch the parabola at A and B, then which of the following is/are correct?
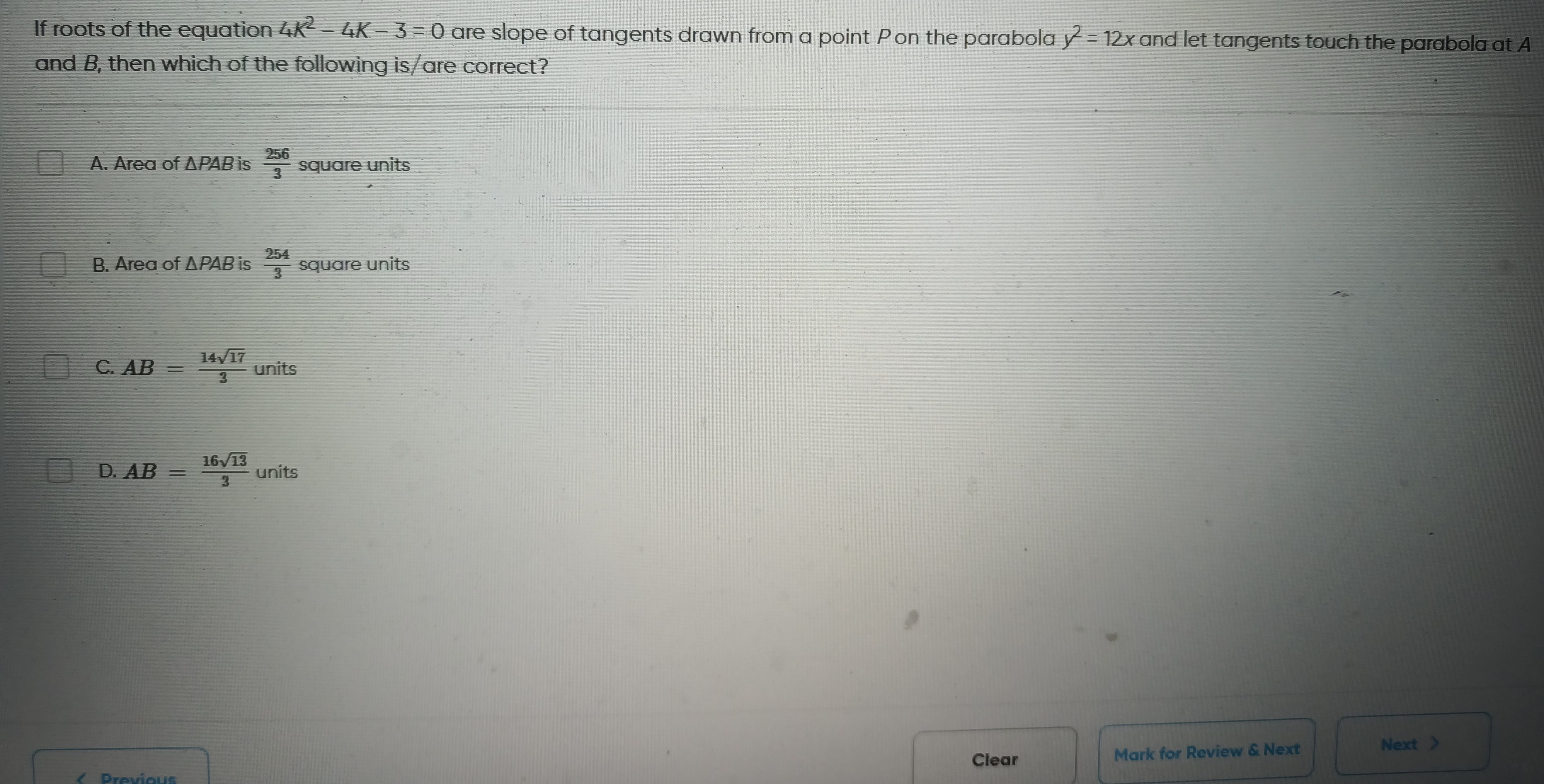
Area of △PAB is 3256 square units
Area of △PAB is 3254 square units
AB=31417 units
AB=31613 units
A, D
Solution
The problem requires us to find the area of a triangle formed by a point P and the points of tangency A and B, where tangents from P are drawn to a parabola, and the length of the chord AB.
Step 1: Find the slopes of the tangents.
The given quadratic equation 4K2−4K−3=0 represents the slopes of the tangents. We solve for K using the quadratic formula K=2a−b±b2−4ac:
K=2(4)−(−4)±(−4)2−4(4)(−3)
K=84±16+48
K=84±64
K=84±8
The two slopes are:
m1=84+8=812=23
m2=84−8=8−4=−21
Step 2: Identify the properties of the parabola.
The equation of the parabola is y2=12x. Comparing this with the standard form y2=4ax, we get 4a=12, so a=3.
Step 3: Find the point P (intersection of tangents).
The equation of a tangent to the parabola y2=4ax with slope m is y=mx+ma.
For m1=23 and a=3:
y=23x+3/23⇒y=23x+2 (Equation 1)
For m2=−21 and a=3:
y=−21x+−1/23⇒y=−21x−6 (Equation 2)
To find point P, we solve Equations 1 and 2:
23x+2=−21x−6
3x+4=−x−12 (multiplying by 2)
4x=−16⇒x=−4
Substitute x=−4 into Equation 1:
y=23(−4)+2=−6+2=−4
So, the point P is (−4,−4).
Step 4: Find the points of tangency A and B.
The coordinates of the point of tangency for a tangent with slope m to y2=4ax are (m2a,m2a).
For m1=23 and a=3:
Point A: ((3/2)23,3/22(3))=(9/43,3/26)=(3×94,6×32)=(34,4)
For m2=−21 and a=3:
Point B: ((−1/2)23,−1/22(3))=(1/43,−1/26)=(3×4,6×(−2))=(12,−12)
So, A=(34,4) and B=(12,−12).
Step 5: Calculate the area of △PAB.
The coordinates are P(−4,−4), A(34,4), B(12,−12).
The area of a triangle with vertices (x1,y1), (x2,y2), (x3,y3) is 21∣x1(y2−y3)+x2(y3−y1)+x3(y1−y2)∣.
Alternatively, for a parabola y2=4ax, if tangents are drawn from an external point P(x1,y1), the area of △PAB is given by 2a(y12−4ax1)3/2.
Using this formula with P(−4,−4) and a=3:
y12−4ax1=(−4)2−4(3)(−4)=16+48=64
Area of △PAB=2(3)(64)3/2=6(64)3=683=6512=3256 square units.
This matches option A.
Step 6: Calculate the length of the chord AB.
Using the distance formula d=(x2−x1)2+(y2−y1)2 for A(34,4) and B(12,−12):
AB=(12−34)2+(−12−4)2
AB=(336−4)2+(−16)2
AB=(332)2+256
AB=91024+256
AB=91024+256×9
AB=91024+2304
AB=93328
To simplify 3328: 3328=16×208=16×16×13=256×13.
So, 3328=256×13=1613.
Therefore, AB=31613 units.
This matches option D.
The correct options are A and D.
