Question

If Rolle's theorem holds for the function $f(x) = x^3 - ax^2 + bx - 4, x \in [1, 2]$ with $f(\frac{4}{3}) = 0$, then 2a - b is equal to:

Answer 1

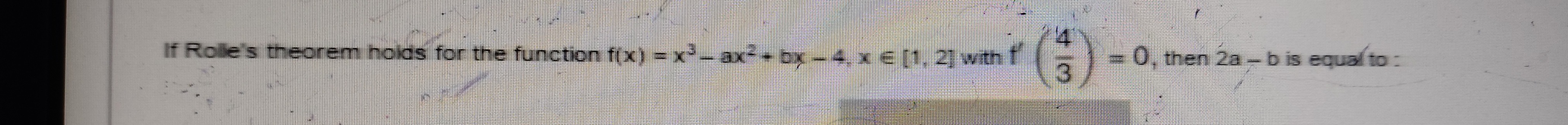
\frac{31}{15}

Answer 2

The problem states that Rolle's theorem holds for the function $f(x) = x^3 - ax^2 + bx - 4$ on the interval $[1, 2]$, and $f(\frac{4}{3}) = 0$. We need to find the value of $2a - b$.

Since Rolle's theorem holds, we know that $f(1) = f(2)$. $f(1) = 1 - a + b - 4 = b - a - 3$ $f(2) = 8 - 4a + 2b - 4 = 2b - 4a + 4$ Setting $f(1) = f(2)$, we get $b - a - 3 = 2b - 4a + 4$, which simplifies to $3a - b = 7$. (Equation 1)

We are also given that $f(\frac{4}{3}) = 0$. Substituting this into the function: $f(\frac{4}{3}) = (\frac{4}{3})^3 - a(\frac{4}{3})^2 + b(\frac{4}{3}) - 4 = 0$ $\frac{64}{27} - \frac{16a}{9} + \frac{4b}{3} - 4 = 0$ Multiplying by 27 to eliminate fractions: $64 - 48a + 36b - 108 = 0$ $-48a + 36b - 44 = 0$ Dividing by -4: $12a - 9b + 11 = 0$, which gives us $12a - 9b = -11$. (Equation 2)

Now we have a system of two linear equations:

1. $3a - b = 7$
2. $12a - 9b = -11$

From Equation 1, we can express $b$ in terms of $a$: $b = 3a - 7$. Substitute this into Equation 2: $12a - 9(3a - 7) = -11$ $12a - 27a + 63 = -11$ $-15a = -74$ $a = \frac{74}{15}$

Now, substitute the value of $a$ back into the expression for $b$: $b = 3a - 7 = 3(\frac{74}{15}) - 7 = \frac{74}{5} - 7 = \frac{74 - 35}{5} = \frac{39}{5}$

So, $a = \frac{74}{15}$ and $b = \frac{39}{5}$. We need to find the value of $2a - b$: $2a - b = 2(\frac{74}{15}) - \frac{39}{5} = \frac{148}{15} - \frac{117}{15} = \frac{31}{15}$

Therefore, $2a - b = \frac{31}{15}$.