Question

If ${\rm P}$ and $Q$ are two distinct points on the parabola, ${y^2} = 4x$ , with parameters $t$ and ${t_1}$ respectively. If the normal at ${\rm P}$ passes through $Q$ , then the minimum value $t_1^2$ is:
A. $8$
B. $4$
C. $6$
D. $2$

Answer 1

Hint : In order to determine the minimum value of $t_1^2$ . First, we compare the given parabola equation ${y^2} = 4x$ with the parameter $t$ and ${t_1}$ . The equation of the normal parametric form ${\rm P}$ to the parabola ${y^2} = - 4ax$ at the point ${\rm P}(a{t^2},2at)$ and $Q(t_1^2,2a{t_1})$ of the parametric equation is $t - yx = 2at + a{t^3}$ and put the value of $a = 1$ into the intersection point then simplify it and get the normal parameter value.

Complete step-by-step answer :
We are given an equation on the parabola ${y^2} = 4(1)x$ and the intersection point ${\rm P}(a{t^2},2at)$ and $Q(t_1^2,2a{t_1})$ of the equation $t - yx = 2at + a{t^3}$
In this equation we are supposed to find out the equation of line which is passing through the point ${\rm P}({t^2},2t)$ and $Q(t_1^2,2{t_1})$ of a normal parametric equation $y + tx = 2t + {t^3}$ . Where, the value $a = 1$ and the parameters $t$ and ${t_1}$ .
The normal equation $tx - y = 2t + {t^3}$ is compared with $y + tx = 2at + a{t^3}$ which is intersect with two distinct point ${\rm P}({t^2},2t)$ and $Q(t_1^2,2{t_1})$ .
The normal parametric form at the point ${\rm P}({t^2},2t)$ of the equation is $tx - y = 2t + {t^3}$ passes through the point $Q(t_1^2,2{t_1})$ .
So the equation is $tt_1^2 - 2{t_1} = 2t + {t^3}$ .
By simplify it in further step, we get
$tt_1^2 - {t^3} = 2t + 2{t_1}$
Now we get
$t(t_1^2 - {t^2}) = 2(t + {t_1})$
When comparing the formula $({a^2} - {b^2}) = (a - b)(a + b)$ with the equation and expand it as $t({t_1} - t)({t_1} + t) = 2(t + {t_1})$ , so, By dividing the common on both side by $(t + {t_1})$
$t({t_1} - t) = 2$
Expanding the factors on RHS, we get
${t_1} = \dfrac{2}{t} + t \geqslant 2\sqrt 2$ . since $\left[ {\dfrac{{\dfrac{2}{t} + t}}{2} \geqslant 2\sqrt 2 } \right]$
We require the minimum value $t_1^2$ is ${(2\sqrt 2 )^2} = 8$
Therefore, the minimum values of $t_1^2$ is $8$ through the equation $tt_1^2 - {t^3} = 2t + 2{t_1}$ and passes the point is ${\rm P}({t^2},2t)$ and $Q(t_1^2,2{t_1})$ .
As a result, the option A: $8$ is the right answer
So, the correct answer is “Option A”.

Note : The graph of the parabola and the normal parametric line is plotted below.
The curve of the parabola is $y = 4x$ and the line that passes through the parabola is $t - yx = 2at + a{t^3}$ .

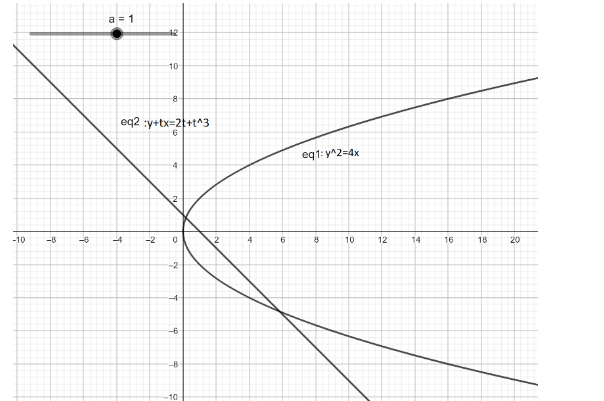
To find the distinct point ${\rm P}(a{t^2},2at)$ and $Q(t_1^2,2a{t_1})$ from the equation $t - yx = 2at + a{t^3}$ . Where the value, $a = 1$ .
Finally we got the minimum value of $t_1^2$ from the equation of normal parameters $t$ and ${t_1}$ .