Question

If resistance is connected in parallel, the voltage across each remains the same.
(A) True
(B) False

Answer 1

The resistors are considered as an electrical component, which contains two terminals and has fixed electrical resistance behavior. When the voltage is connected across two terminals of the resistance, it restricts the flow of electric current through the circuit. Generally, the resistances are connected in parallel and series in the electrical. We are going to determine whether the voltage across each resistor remains the same when the resistors are connected in parallel.

Complete answer:

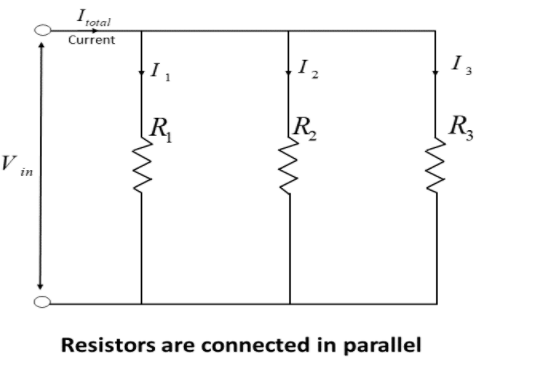
For resistors that are connected in parallel, the number of current paths due to the number of resistors are common voltage input across the two terminals.
The value of voltage across each resistor is the same in the circuit of resistors in parallel. That means the value,
${V_{in}} = {V_1} = {V_2} = {V_3}$
The equivalent resistance in the circuit of resistors is in parallel if the inverse of equivalent resistance is equal to the sum of the inverse of each resistor.
$\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_1}}} = \dfrac{1}{{{R_2}}} = \dfrac{1}{{{R_3}}}$
We can calculate the total current passing through resistor circuit is given by,
${I_{total}} = {I_1} + {I_2}$
We know that from ohm’s law, $V = IR$
Where V-voltage across two terminals
$I$ - current passing through the circuit
$R$ - resistance
The current passing through each resistor is given by,
${I_1} = \dfrac{{{V_1}}}{{{R_1}}},{I_2} = \dfrac{{{V_2}}}{{{R_2}}},{I_3} = \dfrac{{{V_3}}}{{{R_3}}}$,$\left( {{V_{in}} = {V_1} = {V_2} = {V_3}} \right)$
From the above discussions, we came to know that the voltage across each resistor remains the same when the resistors are connected in parallel.
Therefore, the answer is option (A) True.

Note: The total current passing through the circuit is also calculated using the equivalent resistance is given by,${I_{total}} = \dfrac{{{V_{in}}}}{{{R_{eq}}}}$ where ${V_{in}}$- input voltage across two terminals,${R_{eq}}$- equivalent resistance in the circuit. For the resistance to be connected in series, the current passing through all the resistors is the same. But the voltage across each resistor drops by the resistance value in the circuit.