Question
Question: If range of the function $f(x) = log_{\frac{1}{\sqrt{3}}}(\sqrt{2}(sinx+cosx)+3)$ is $[a,b]$ then fi...
If range of the function f(x)=log31(2(sinx+cosx)+3) is [a,b] then find value of (a2+b2).
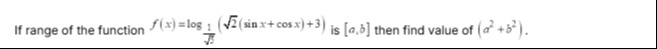
4(log35)2
Solution
The given function is f(x)=log31(2(sinx+cosx)+3).
Let the argument of the logarithm be g(x)=2(sinx+cosx)+3.
First, we simplify the trigonometric expression sinx+cosx. We can write sinx+cosx=12+12(21sinx+21cosx)=2(sinxcos(4π)+cosxsin(4π))=2sin(x+4π).
So, 2(sinx+cosx)=2⋅2sin(x+4π)=2sin(x+4π).
Now, the argument of the logarithm is g(x)=2sin(x+4π)+3.
The range of sin(θ) for any real θ is [−1,1].
Thus, the range of sin(x+4π) is [−1,1].
The range of 2sin(x+4π) is [2(−1),2(1)]=[−2,2].
The range of g(x)=2sin(x+4π)+3 is [−2+3,2+3]=[1,5].
For the logarithm f(x)=log31(g(x)) to be defined, the argument g(x) must be positive. The range of g(x) is [1,5], and all values in this range are positive, so the logarithm is defined for all real x.
The base of the logarithm is b=31. Since 0<31<1, the logarithm function y=logb(u) is a strictly decreasing function of u.
This means that the minimum value of g(x) corresponds to the maximum value of f(x), and the maximum value of g(x) corresponds to the minimum value of f(x).
The minimum value of g(x) is gmin=1.
The maximum value of g(x) is gmax=5.
The maximum value of f(x) is fmax=log31(gmin)=log31(1).
Since logb(1)=0 for any valid base b, fmax=0.
The minimum value of f(x) is fmin=log31(gmax)=log31(5).
We can write the base 31 as 3−1/2.
fmin=log3−1/2(5). Using the property logbk(m)=k1logb(m), we get:
fmin=−1/21log3(5)=−2log3(5).
The range of the function f(x) is [fmin,fmax]=[−2log3(5),0].
The problem states that the range is [a,b].
Comparing the ranges, we have a=−2log3(5) and b=0.
We need to find the value of a2+b2.
a2=(−2log3(5))2=(−2)2(log3(5))2=4(log3(5))2.
b2=02=0.
a2+b2=4(log3(5))2+0=4(log3(5))2.
The final answer is 4(log35)2.
Explanation of the solution:
- Simplify 2(sinx+cosx) to 2sin(x+π/4).
- Find the range of the argument of the logarithm: g(x)=2sin(x+π/4)+3. The range of sin(x+π/4) is [−1,1], so the range of g(x) is [2(−1)+3,2(1)+3]=[1,5].
- The base of the logarithm 1/3 is between 0 and 1, so the logarithm is a decreasing function.
- The range of f(x)=log1/3(g(x)) is [log1/3(max(g(x))),log1/3(min(g(x)))]=[log1/3(5),log1/3(1)].
- Calculate the values: log1/3(1)=0 and log1/3(5)=log3−1/2(5)=−2log3(5).
- The range is [−2log3(5),0]. Thus, a=−2log3(5) and b=0.
- Calculate a2+b2=(−2log3(5))2+02=4(log3(5))2.
Answer: 4(log35)2
