Question

If range of the function $f(x) = (\cos^{-1} \frac{x}{2})^2 + \pi \sin^{-1} \frac{x}{2} - (\sin^{-1} \frac{x}{2})^2 + \frac{\pi^2}{12}(x^2 + 6x + 8)$ is $[a\pi^2, b\pi^2]$, then find the value of $2(a+b)$.

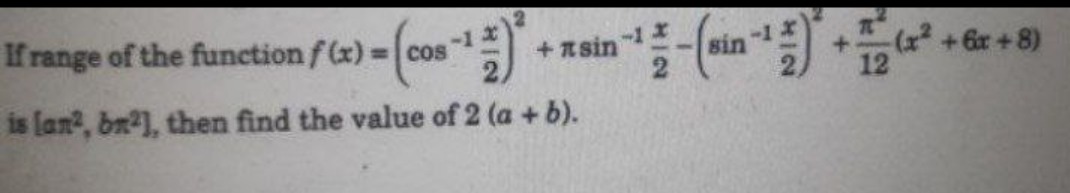
Answer 1

5

Answer 2

The domain of $f(x)$ is $[-2, 2]$. Using $\cos^{-1} \frac{x}{2} = \frac{\pi}{2} - \sin^{-1} \frac{x}{2}$, the function simplifies to $f(x) = \frac{\pi^2}{4} + \frac{\pi^2}{12}(x^2 + 6x + 8)$. Let $g(x) = x^2 + 6x + 8$. On $[-2, 2]$, $g(x)$ is increasing, with range $[g(-2), g(2)] = [0, 24]$. The range of $f(x)$ is $[\frac{\pi^2}{4} + \frac{\pi^2}{12}(0), \frac{\pi^2}{4} + \frac{\pi^2}{12}(24)] = [\frac{\pi^2}{4}, \frac{9\pi^2}{4}]$. Comparing with $[a\pi^2, b\pi^2]$, we get $a = \frac{1}{4}$ and $b = \frac{9}{4}$. Therefore, $2(a+b) = 2(\frac{1}{4} + \frac{9}{4}) = 5$.