Question

If R=\left\\{ \left( x,y \right)|x+2y=8 \right\\} is a relation on N, find the range of R.

Answer 1

To solve this question, we should know the meaning of N. N is the notation we use for natural numbers and the range of N is $N=\left( 1,2,3......... \right)$. We are given the relation between two variables x and y as $x+2y=8$ and we are asked to find the values of x and y. We know that x and y are positive numbers as they belong to natural numbers set. We should substitute different values of y which are in the range of natural numbers, to get the values of x in the same range. For example, if we substitute y = 1, from the relation, we get $x+2\times 1=8\Rightarrow x=6$. So, $\left( 6,1 \right)$ is an element of the set R. We know that we cannot go beyond y = 4, because we will get a negative value. So the maximum value that we can use is y = 4 and check if x also lie within the range on N.

Complete step by step answer:
We are given a relation between x and y as $x+2y=8$ and the relation is defined in the set of N which is a natural numbers set.
We know that $N=\left( 1,2,3......... \right)$
We should substitute different values of y from natural numbers and get different values of x in the natural numbers set.
Let us consider that $y=1$
We can get the value of x as
$\begin{aligned} & x+2\times 1=8 \\\ & x=6 \\\ \end{aligned}$
So, $\left( x,y \right)=\left( 6,1 \right)$ is an element in the relation R.
Let us consider that $y=2$
We can get the value of x as
$\begin{aligned} & x+2\times 2=8 \\\ & x=4 \\\ \end{aligned}$
So, $\left( x,y \right)=\left( 4,2 \right)$ is an element in the relation R.
Let us consider that $y=3$
We can get the value of x as
$\begin{aligned} & x+2\times 3=8 \\\ & x=2 \\\ \end{aligned}$
So, $\left( x,y \right)=\left( 2,3 \right)$ is an element in the relation R.
Let us consider that $y=4$
We can get the value of x as
$\begin{aligned} & x+2\times 4=8 \\\ & x=0 \\\ \end{aligned}$
We know the range of natural numbers is $N=\left( 1,2,3......... \right)$ and $x=0$ is not in the set of natural numbers.
So, $\left( x,y \right)=\left( 0,4 \right)$ is not an element in the relation R.
We can see that further increase of y leads to a negative value in x. Those solutions are not in the solution set.

$\therefore$The range of R is R=\left\\{ \left( 6,1 \right),\left( 4,2 \right),\left( 2,3 \right) \right\\}

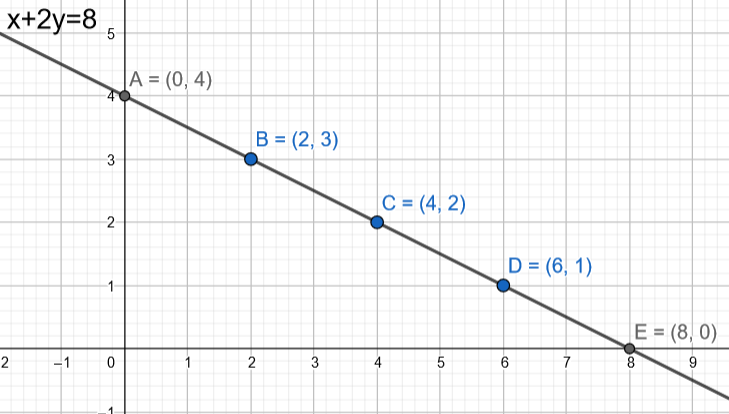
Note: We can also use the graphical method to get the answer. The relation $x+2y=8$ is a straight line which has an infinite number of solutions. But, we are restricted to natural numbers and that means, the positive integral solutions. In the figure, the points B, C, D are the elements in the relation R. Students should note that the points A and E are not in the solution set. Students might confuse that natural numbers also include 0 and they will also include the points A and E in the solution. We should be clear that 0 is not included in natural numbers.