Question

If R is the relation ‘less than’ from $A=\\{1,2,3,4,5\\}$ to $B=\\{1,4\\}$, the set of ordered pairs corresponding to R, then the inverse of R is
(a){(3,1), (3,2), (3,3)}
(b){(4,1), (4,2), (4,3)}
(c){(4,3), (4,4), (4,5)}
(d){(1,3), (2,4), (3,5)}

Answer 1

Convert the sets given in the roster form into sets in set builder form. Generalize the given relation and then find its inverse. Make necessary conversions to obtain the answer in the form of the given options. Draw diagrams to represent the functions and the relations.

Complete step-by-step answer:
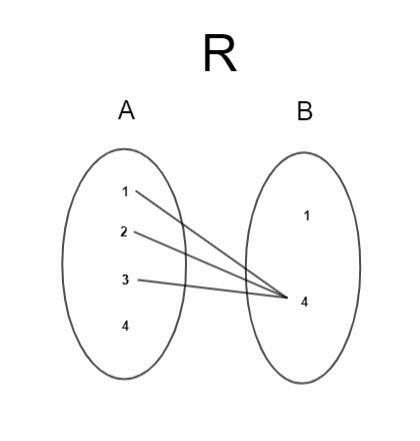
Let us first represent the given relation R, ‘less than’ from $A=\\{1,2,3,4,5\\}$ to $B=\\{1,4\\}$ in a general form.
Let $x$ be an element in set$A$ and $y$be an element in set $B$. According to the question, R is a relation from set$A$ to set $B$, where elements are paired using the condition that the element in set$A$ is less than the element in set $B$.
The above statement can be represented in a more generalized form (Known as the set builder form), which is as follows,
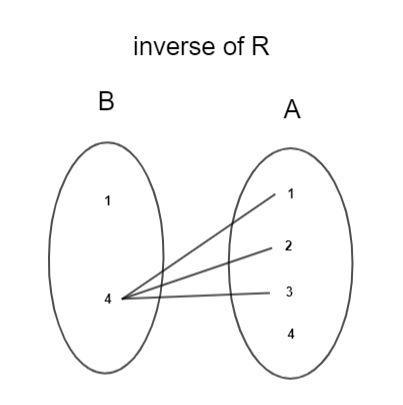
R=\\{(x,y):xThis can also be written in another form (Known as the roster form), which is as follows, R=\{(1,4),(2,4),(3,4)\}$(We have to note that our options are in this form) We have to find the inverse of$R=\{(x,y):xWe know that R is a relation from set A to B ($(x,y):xSince the relation is from B to A we interchange$xand $$y$$ to obtain the equation for{{R}^{-1}}$.${{R}^{-1}}=\{(x,y):yConverting the above set builder form into roster form, we obtain,
${{R}^{-1}}=\\{(4,1),(4,2),(4,3)\\}$
Hence the inverse of R is {(4,1), (4,2), (4,3)}

So, the correct answer is “Option (b)”.

Note: The relation is from $A$ to$B$, that is, $A$ is the domain of this relation and $B$ is the co-domain. In this case, an element in$A$, say $x$ is called the pre-image of an element in$B$, say$y$. And in the same way $y$ is called the image of$x$. This is of course if and only if $x$ is related to$y$.
We can represent the relation in the form of diagrams and solve the question.