Question

If r is the radius of incircle and ${{r}_{1}},{{r}_{2}},{{r}_{3}}$ are the radii of the ex-circles of the triangle ABC opposite to angles $A,B,C$ respectively then find $B$ if $r{{r}_{2}}={{r}_{1}}{{r}_{3}}$. $$$$

Answer 1

We substitute $r=\dfrac{\Delta }{s},{{r}_{1}}=\dfrac{\Delta }{\left( s-a \right)},{{r}_{2}}=\dfrac{\Delta }{\left( s-b \right)},{{r}_{3}}=\dfrac{\Delta }{\left( s-c \right)}$ where $a,$ $b$,$c$ are the lengths of the sides BC, AC,AB respectively, $s$ is the semi-perimeter of the triangle and $\Delta$ is the area of the triangle in the given equation $r{{r}_{2}}={{r}_{1}}{{r}_{3}}$ . We proceed to simplify the equation until we have to use $r=\left( s-b \right)\tan \dfrac{B}{2}$ and then we solve for $B$ to get the measurement of $B$.

Complete step-by-step solution:
__
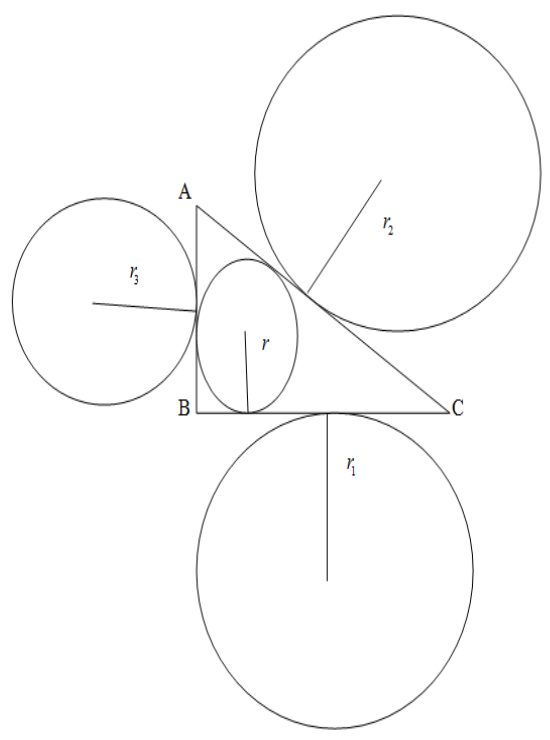
We are given that $r$ is the radius of in-circle and ${{r}_{1}},{{r}_{2}},{{r}_{3}}$ are the radii of the ex-circles of the triangle ABC opposite to angles $A,B,C$ respectively. We know from the formula that
$r=\dfrac{\Delta }{s},{{r}_{1}}=\dfrac{\Delta }{\left( s-a \right)},{{r}_{2}}=\dfrac{\Delta }{\left( s-b \right)},{{r}_{3}}=\dfrac{\Delta }{\left( s-c \right)}....(1)$
Where the $a,$ $b$,$c$ are the lengths of the sides BC, AC, AB respectively, $s$ is the semi-perimeter of the triangle and $\Delta$ is the area of the triangle.
We also know the formula involving tangent and length of the sides as
$r=\left( s-a \right)\tan \dfrac{A}{2}=\left( s-b \right)\tan \dfrac{B}{2}=\left( s-c \right)\tan \dfrac{C}{2}...(2)$
We know that the area of the triangle with semi-perimeter $s$ and the lengths of the sides $a,$ $b$,$c$ is
$\Delta =\sqrt{s\left( s-b \right)\left( s-a \right)\left( s-c \right)}...(3)$

We are given in the question that
$r{{r}_{2}}={{r}_{1}}{{r}_{3}}$
We are asked to find the measurement of the angle B. We put the values of $r,{{r}_{1}},{{r}_{2}},{{r}_{3}}$ in terms of area, semi-perimeter and side in the given equation and get ,

& r{{r}_{2}}={{r}_{1}}{{r}_{3}} \\\ & \Rightarrow \dfrac{\Delta }{s}\times \dfrac{\Delta }{s\left( s-b \right)}=\dfrac{\Delta }{s\left( s-a \right)}\times \dfrac{\Delta }{s\left( s-c \right)} \\\ \end{aligned}$$ We can divide $\Delta $ both side and then cross multiply to get , $$\begin{aligned} & r{{r}_{2}}={{r}_{1}}{{r}_{3}} \\\ & \Rightarrow \dfrac{\Delta }{s}\times \dfrac{\Delta }{\left( s-b \right)}=\dfrac{\Delta }{\left( s-a \right)}\times \dfrac{\Delta }{\left( s-c \right)} \\\ & \Rightarrow s\left( s-b \right)=\left( s-a \right)\left( s-c \right) \\\ \end{aligned}$$ We now multiply $s\left( s-b \right)$ both side and get , $$\Rightarrow {{\left( s\left( s-b \right) \right)}^{2}}=s\left( s-b \right)\left( s-a \right)\left( s-c \right)$$ We use the formula (3) and replace the right hand side with ${{\Delta }^{2}}$. SO we have $$\Rightarrow {{\left( s\left( s-b \right) \right)}^{2}}={{\Delta }^{2}}$$ We now divide ${{\left( s\left( s-b \right) \right)}^{2}}$ both side and get , $$\Rightarrow {{\left( \dfrac{\Delta }{s\left( s-b \right)} \right)}^{2}}=1$$ We use the formula (2) and get , $$\Rightarrow {{\left( \tan \dfrac{B}{2} \right)}^{2}}=1$$ We solve above quadratic equation and get , $$\begin{aligned} & \Rightarrow \tan \dfrac{B}{2}=1,\tan \dfrac{B}{2}=-1 \\\ & \Rightarrow \dfrac{B}{2}=\dfrac{\pi }{4},\dfrac{B}{2}=\dfrac{5\pi }{4} \\\ & \Rightarrow B=\dfrac{\pi }{2},B=\dfrac{10\pi }{4} \\\ \end{aligned}$$ **We reject the result $B=\dfrac{10\pi }{4}$ because in triangle no angle can be greater than $\pi .$ So the $B=\dfrac{\pi }{2}={{90}^{\circ }}$ , a right angle.** **Note:** We note that the incircle which touches all sides in the interior of the triangle has its center called incentre as the point of intersection of angle bisectors while excircles touch only 1 side in the exterior with center at the exterior known as excentre. The general solution for $\tan x=\tan \alpha $ is $x=n\pi +\alpha $ where $n$ is an integer. We have rejected other values because our problem was limited to a triangle.