Question

If R is the radius of circumcentre of $\Delta ABC,$ then $R=\dfrac{abc}{4S}$
(A) True
(B) False

Answer 1

Hint: Use area of triangle formula, where two sides of triangle and angle between them is given. Use sine rule related with circumradius to get the given relation.

Complete step-by-step answer:
Here, we have given R as a radius of circumcircle i.e. circumradius and need to prove the relation;
$R=\dfrac{abc}{4S}$……………….(1)
Where (a, b, c) are sides of the triangle as denoted in the diagram.

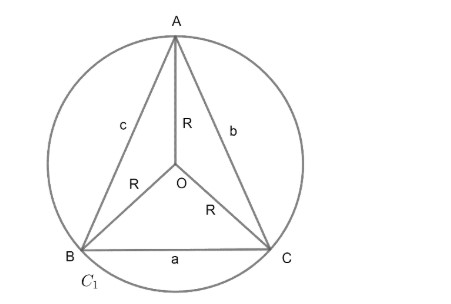
Where O is the centre of the circle C, which is circumscribing the triangle ABC.
R = Circumradius of triangle ABC.
We can write sine rule in $\Delta ABC$ involving circumradius R as;
$\dfrac{\sin A}{a}=\dfrac{\sin B}{b}=\dfrac{\sin C}{c}=\dfrac{1}{2R}..............\left( 2 \right)$
As we have a formula of area with involvement of two sides and angle between them.
Let the area be represented by S.
$Area=S=\dfrac{1}{2}bc\sin A=\dfrac{1}{2}ab\sin C=\dfrac{1}{2}ac\sin B........\left( 3 \right)$
Now, from equation (2) and (3), we can write an equation with respect to one angle as
$\dfrac{\sin A}{a}=\dfrac{1}{2R}\text{ and }S=\dfrac{1}{2}bc\sin A$
Substituting value of sin A from the relation $\dfrac{\sin A}{a}=\dfrac{1}{2R}\text{ to }S=\dfrac{1}{2}bc\sin A$, we get;
As $\sin A=\dfrac{a}{2R}$ from the first relation, now putting value of sin A in $S=\dfrac{1}{2}bc\sin A$, we get
$\begin{aligned} & S=\dfrac{1}{2}bc\dfrac{a}{2R} \\\ & S=\dfrac{abc}{4R} \\\ \end{aligned}$
Transferring R to other side, we get;
$R=\dfrac{abc}{4S}$
Hence, the relation given in the problem is true.
Note: One can go wrong with the formula of area of the triangle. One can apply heron’s formula for proving i.e.
$\begin{aligned} & S=\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)} \\\ & s=\dfrac{a+b+c}{2} \\\ \end{aligned}$
Which will make the solution very complex.
One can go wrong while writing sine rule as;
$\dfrac{\sin A}{a}=\dfrac{\sin B}{b}=\dfrac{\sin C}{c}=\dfrac{2R}{1}$ which is wrong.
Correct equation of sine rule will be,
$\dfrac{\sin A}{a}=\dfrac{\sin B}{b}=\dfrac{\sin C}{c}=\dfrac{1}{2R}$.