Question

If $R$ is the horizontal range for an inclination and $h$ is the maximum the height reached by the projectile, then the maximum range is given by-
$(A)\dfrac{{{R^2}}}{{8h}} - 2h$
$(B)\dfrac{{{R^2}}}{{8h}} + 2gh$
$(C)\dfrac{{{R^2}}}{{8h}} + 2h$
$(D)\dfrac{{{R^2}}}{{8h}}$

Answer 1

Draw a clean diagram of projectile motion and clarify the vertical and horizontal motion of the object by dividing the initial velocity into two components.
Find the value of maximum height that the object will gain using the vertical equation of motion. Note that the final velocity in the highest point will be zero.
Use the formula of horizontal range. Note that the object will travel with a uniform velocity horizontally.
State a relation between the maximum height and maximum horizontal range. Note that the maximum horizontal range can be obtained by maximizing the sine of the angle.

Formula used:
From the equation of motion $\Rightarrow {v^2} = {u^2} - 2gh$, we get
$\Rightarrow h = \dfrac{{{u^2}{{\sin }^2}\theta }}{{2g}}$ , For the vertical motion the initial velocity $u\sin \theta$
The horizontal distance $R = u\cos \theta \times T$, the object travels with a uniform velocity $u\cos \theta$ horizontally.
Where, $T = \dfrac{{2u\sin \theta }}{g}$
${R_{\max }} = \dfrac{{{u^2}}}{g}$

Complete step by step answer:

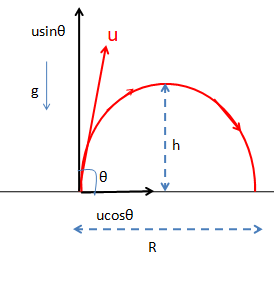
The initial velocity $u$ has two components along vertical and horizontal.
Here, $u\sin \theta$ is the vertical component and also, $u\cos \theta$ is the horizontal component.
For the vertical motion the initial velocity $u\sin \theta$
The final velocity, $v = 0$
Then if the maximum height be $h$,
Then, $0 = {\left( {u\sin \theta } \right)^2} - 2gh$ [ from the equation of motion $\Rightarrow {v^2} = {u^2} - 2gh$ ]
$\Rightarrow h = \dfrac{{{u^2}{{\sin }^2}\theta }}{{2g}}..............(1)$

Now the horizontal range be $R$
So at the time, $T$ the object will travel the horizontal distance $R$
Since the object travels with a uniform velocity $u\cos \theta$ horizontally and covers the distance $R$,
Hence, $R = u\cos \theta \times T$
Where, $T = \dfrac{{2u\sin \theta }}{g}$
$\therefore R = u\cos \theta \times \dfrac{{2u\sin \theta }}{g}$
$\Rightarrow R = \dfrac{{{u^2}\sin 2\theta }}{g}.............(2)$

Now, from eq $(1)$ and $(2)$ we get, $\dfrac{h}{R} = \dfrac{{{{\sin }^2}\theta }}{{2\sin 2\theta }}$
$\Rightarrow \dfrac{h}{R} = \dfrac{{{{\sin }^2}\theta }}{{4\sin \theta \cos \theta }}$
$\Rightarrow \dfrac{h}{R} = \dfrac{{\sin \theta }}{{4\cos \theta }}$
$\Rightarrow \dfrac{h}{R} = \dfrac{1}{4}\tan \theta$
$\Rightarrow \tan \theta = \dfrac{{4h}}{R}$

Now if we draw a right angle triangle by taking $\theta$ the acute angle, $4h$ be the perpendicular, and $R$be the base,
$\sin \theta = \dfrac{{4h}}{{\sqrt {16{h^2} + {R^2}} }}$
Hence by putting the value of $\sin \theta$ we get from eq. $(1)$, $\Rightarrow h = \dfrac{{{u^2}}}{g} \times \dfrac{{16{h^2}}}{{2(16{h^2} + {R^2})}}..........(3)$
When the value of $\sin 2\theta$ the highest, the horizontal range $R$ will also be highest,
since, the highest value of $\sin 2\theta = 1$ , ${R_{\max }} = \dfrac{{{u^2}}}{g}......(4)$
now, from eq. $(3)$ and $(4)$ we get,
$\Rightarrow h = {R_{\max }} \times \dfrac{{16{h^2}}}{{2(16{h^2} + {R^2})}}$
$\Rightarrow {R_{\max }} = \dfrac{{2h(16{h^2} + {R^2})}}{{16{h^2}}}$
$\Rightarrow {R_{\max }} = \dfrac{{(16{h^2} + {R^2})}}{{8h}}$
$\Rightarrow {R_{\max }} = 2h + \dfrac{{{R^2}}}{{8h}}$
So, the maximum range will be, $\Rightarrow {R_{\max }} = 2h + \dfrac{{{R^2}}}{{8h}}$

Hence, the correct answer is option (C).

Note: The locus of a projectile is given by, $y = x\tan \theta - \dfrac{g}{{2{u^2}{{\cos }^2}\theta }}{x^2}$

This equation is the form of the equation of a parabola, $y = ax + b{x^2}$
So, the locus of a projectile is Parabolic.