Question

If $R$ and $H$ are the horizontal range and maximum height attained by a projectile then its speed of projection is:

& A.\sqrt{2gR+\dfrac{4{{R}^{2}}}{gH}} \\\ & B.\sqrt{2gh+\dfrac{{{R}^{2}}g}{8H}} \\\ & C.\sqrt{2gH+\dfrac{8H}{gR}} \\\ & D.\sqrt{2gH+\dfrac{{{R}^{2}}}{H}} \\\ \end{aligned}$$

Answer 1

A body experiences a projectile motion when the object is projected at an inclination from the ground. Then the body follows a curved path, which is parabolic in nature and is called the ballistic trajectory. Then the distance covered by the body along the x and y-axis respectively is given as, $R$ and $H$ which is the maximum horizontal range and maximum height attained by the object.

Formula used:
$v^{2}-u^{2}=2as$ and $s=ut+\dfrac{1}{2}at^{2}$

Complete step-by-step answer:
Let $u$ be the initial velocity of the body which is projected at an angle $\theta$ from the horizontal. Let $H$ and $R$ be the maximum distances along the x and y-axis respectively, during the time of flight $T$. Then the initial velocity $u$ can be resolved into two components along the x and y axis respectively.

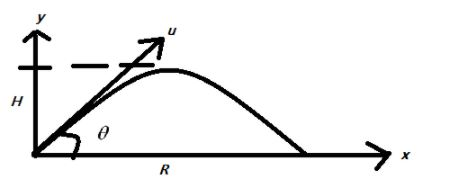
Then along the y-axis we have, the maximum height $H$ , initial velocity $u_{y}=usin\theta$ , final velocity $v_{y}=0$ and acceleration $a_{y}=-g$
Then we can write, $v^{2}-u^{2}=2as$ or $0-(usin\theta)^{2}=2\times (-g)\times H$
Or $usin\theta=\sqrt{2gH}$
From $s=ut+\dfrac{1}{2}at^{2}$ , let us consider the he half flight, where $s=-H$ and $t=\dfrac{T}{2}$
Then we get, $-H=0+\dfrac{1}{2}(-g)\left(\dfrac{T}{2}\right)^{2}$
Or, $T=\sqrt{\dfrac{8H}{g}}$
Similarly, along the x-axis we have, the maximum range $R$ and the initial velocity $u_{x}=ucos\theta$ . The time of flight $T$ can be given as $T=\dfrac{R}{ucos\theta}$
Or, $ucos\theta=\dfrac{R}{ T}$
This is similar to $vel=\dfrac{distance}{time}$
Substituting for $T$ we get, $ucos\theta=R\times\sqrt{\dfrac{g}{8H}}$
Let us square and add $(usin\theta)^{2}+(ucos\theta)^{2}=u^{2}$ as $sin^{2}\theta+cos^{2}\theta=1$
Or $u^{2}=(\sqrt{2gH})^{2}+\left(R\times\sqrt{\dfrac{g}{8H}}\right )^{2}$
Or, $u=\sqrt{2gH+\dfrac{R^{2}g}{8H}}$

So, the correct answer is “Option B”.

Note: When the object is on the air,the only force acting on the body is the force due to gravitation, which pulls the object back to the surface at the speed of acceleration due to gravity. Note that the range of the projected body is greater than the distance the body will cover, when dropped from the same height.