Question

If $R$ and $H$ are the horizontal range and maximum height attained by a projectile, then its speed of projection is
(A). $\sqrt {2gR + \dfrac{{4{R^2}}}{{gH}}}$
(B). $\sqrt {2gh + \dfrac{{{R^2}g}}{{8H}}}$
(C). $\sqrt {2gH + \dfrac{{8H}}{{Rg}}}$
(D). $\sqrt {2gH + \dfrac{{{R^2}}}{H}}$

Answer 1

- Hint: You can start by using the equation ${v^2} - {u^2} = 2as$ for the motion of the body to the highest point(A to B) and find the value of $v\sin \theta$. Then use the equation $s = ut + \dfrac{1}{2}a {t^2}$ for the motion of the body to the highest point(A to B) and find the value of $T$. Then use the equation $R = v\cos \theta \times T$ to find the value of $v\cos \theta$. Then add the squares of $v\sin \theta$ and $v\cos \theta$ to reach the solution.

Complete step-by-step answer:
Let’s take the velocity of the projection and angle of projection with the horizontal as $v$ and $\theta$ respectively.

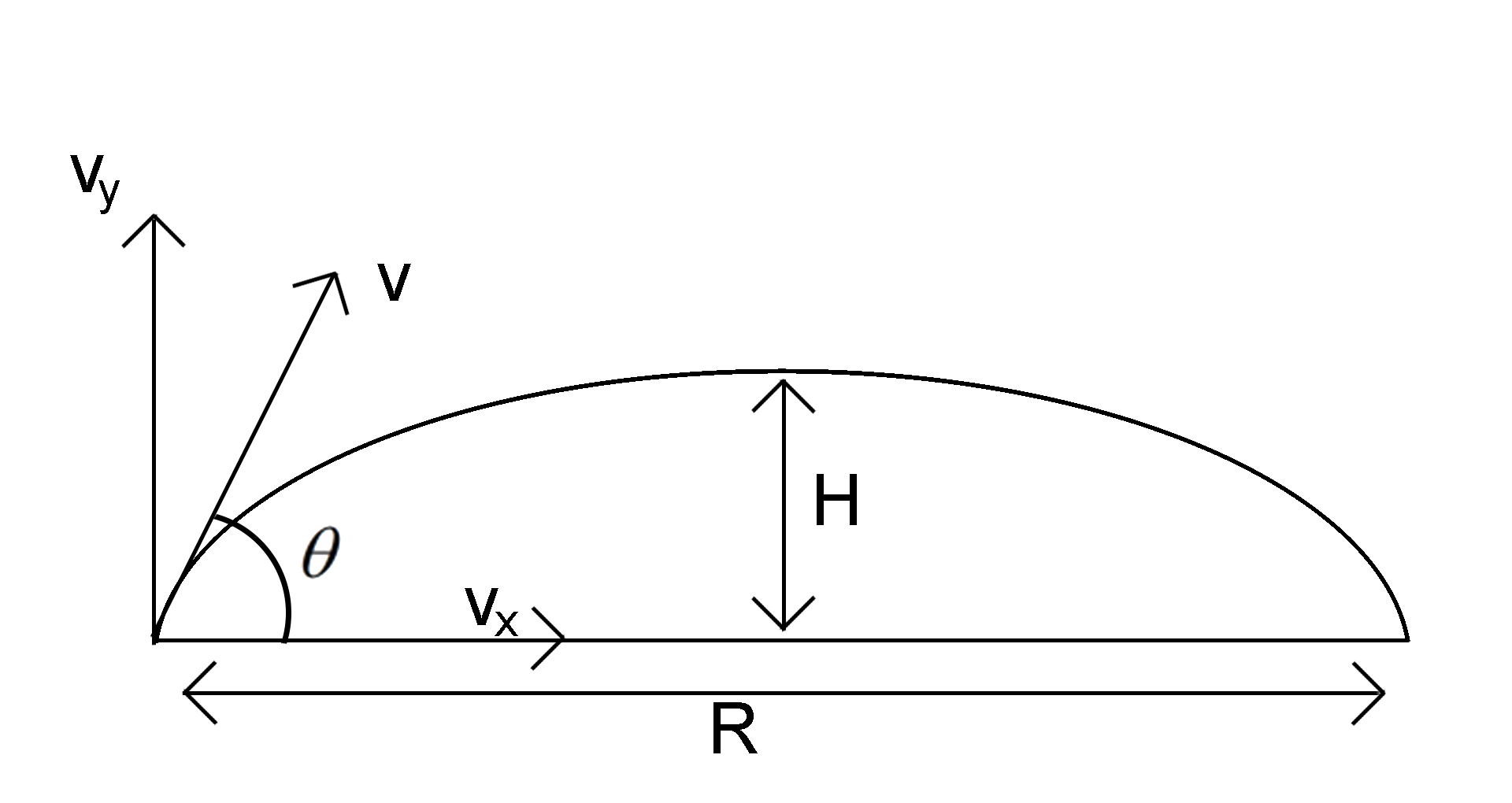
The projectile has some initial vertical velocity (${v_y} = v\sin \theta$), due to this initial vertical velocity the projectile rises up in the air to the maximum height where the velocity becomes zero due the gravitational pull of the earth.
So for vertical motion from point A to point B
$u = v\sin \theta$, $v = 0$,$a = - g$ and $s = H$
Using the third equation of motion given by Newton
${v^2} - {u^2} = 2as$
$0 - {v^2}{\sin ^2}\theta = 2 \times ( - g)H$
$v\sin \theta = \sqrt {2gH}$ (Equation 1)
From point A to B the projectile goes up and from point B to C the projectile goes down. The time taken in going from point A to B is equal to the time taken by projectile in going from point B to C.
Let the total time taken by projectile joining from point A to point C be T.
So, for vertical motion of projectile from point B to C
$t = \dfrac{T}{2}$,$s = H$,$u = 0$ and $a = g$
Now, applying second equation of motion
$s = ut + \dfrac{1}{2}a{t^2}$
$H = 0 \times \dfrac{T}{2} + \dfrac{1}{2}g{\left( {\dfrac{T}{2}} \right)^2}$
$H = \dfrac{1}{8}g{T^2}$
$T = \sqrt {\dfrac{{8H}}{g}}$(Equation 2)
We know that
$R = v\cos \theta \times T$
Here $R =$Range and $v\cos \theta =$horizontal component of velocity
$R = v\cos \theta \sqrt {\dfrac{{8H}}{g}}$(From Equation 2)
$v\cos \theta = R\sqrt {\dfrac{g}{{8H}}}$(Equation 3)
Squaring equation 1 and 3 and adding them, we get
${v^2}{\sin ^2}\theta + {v^2}{\cos ^2}\theta = 2gH + \dfrac{{{R^2}g}}{{8H}}$
{v^2} = 2gH + \dfrac{{{R^2}g}}{{8H}}$$$$(\because {\sin ^2}\theta + {\cos ^2}\theta )
$v = \sqrt {2gH + \dfrac{{{R^2}g}}{{8H}}}$
Hence, option B is the correct choice.

Note: In the solution we mentioned that the time taken by the projectile in going from point A to point B is equal to the time taken by the projectile in going from point B to C. It is quite obvious as velocity at point A and C will be same in magnitude but in the opposite direction and the acceleration is constant throughout, i.e. $g$.