Question

If $R=1\Omega$ , the current in the branch x is then ,

& A)\dfrac{1}{2}A \\\ & B)0A \\\ & C)\dfrac{4}{5}A \\\ & D)1A \\\ \end{aligned}$$

Answer 1

First try to simplify the circuit in series and parallel combination so that circuit gets simplified. Then apply Ohm’s Law in this simplified circuit ,if current get divided between branches then potential is same then they are connected in parallel similarly when current is same then they are in series.

Complete step-by-step answer:
Mark all the resistance as R1; R2; R3; R4 respectively.

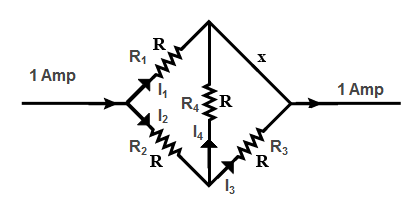
Since ${{R}_{3}}\parallel {{R}_{4}}$ (Parallel Combination) .So net resistance is represented by ${{R}^{'}}$.
Apply formula for parallel combination of two resistances and we get, ${{R}^{'}}=\dfrac{{{R}_{3}}{{R}_{4}}}{{{R}_{3}}+{{R}_{4}}}$
On putting the value of all resistances and all values are same we get
$\Rightarrow {{R}^{'}}=\dfrac{{{R}^{2}}}{2R}$
$\therefore {{R}^{'}}=\dfrac{R}{2}$
So net resistance becomes half of the initial value.
Now this resistance${{R}^{'}}$ is parallel to ${{R}_{2}}$.So net resistance of this
combination is represented by ${{R}_{X}}$.
So apply series formula for combination of resistance, we get
${{R}_{X}}={{R}^{'}}+{{R}_{2}}$
$\Rightarrow {{R}_{X}}=R+\dfrac{R}{2}$
$\therefore {{R}_{X}}=\dfrac{3R}{2}$
Now in place of ${{R}_{2}}$ we can put${{R}_{X}}$. Now see in the figure current in branches get divided into several parts. Now we consider the figure and see that ${{R}_{1}}\And {{R}_{X}}$ are connected in parallel because current gets divided between them .So potential difference becomes equal .
Now we apply ohm’s law we get
Potential of Resistance ${{R}_{1}}$=Potential of Resistance ${{R}_{X}}$
\Rightarrow $$$${{I}_{1}}{{R}_{1}}={{I}_{2}}{{R}_{X}}
Put the value of ${{R}_{X}}$,we get
$\Rightarrow {{I}_{1}}R={{I}_{2}}\dfrac{3R}{2}$
$\Rightarrow {{I}_{1}}=\dfrac{3}{2}{{I}_{2}}$(Equation1)
According to circuit we can write,
${{I}_{1}}+{{I}_{2}}=1$
Put the value of ${{I}_{1}}$from equation 1in this equation ,we get

& \Rightarrow \dfrac{3}{2}{{I}_{2}}+{{I}_{2}}=1 \\\ & \Rightarrow \dfrac{5}{2}{{I}_{2}}=1 \\\ & \therefore {{I}_{2}}=\dfrac{2}{5}A \\\ \end{aligned}$$ Now we put this value in equation 1 we get $$\begin{aligned} & \Rightarrow {{I}_{1}}=\dfrac{3}{2}\times \dfrac{2}{5} \\\ & \therefore {{I}_{1}}=\dfrac{3}{5}A \\\ \end{aligned}$$ This current $${{I}_{2}}$$ is further divided into two branches having current $${{I}_{3}}\And {{I}_{4}}$$,Since resistance is same in both the branches so this current is divided equally in two halves . So the value of $${{I}_{3}}\And {{I}_{4}}$$becomes $$\dfrac{1}{5}A$$. So , $${{I}_{3}}={{I}_{4}}=\dfrac{1}{5}A$$ Now see in the figure current passes through this branch X will be $${{I}_{1}}\And {{I}_{4}}$$. So current in branch X is given by = $${{I}_{1}}+{{I}_{4}}$$ Current in branch X will become $$=\dfrac{3}{5}+\dfrac{1}{5}=\dfrac{4}{5}A$$ Now in branch X will become $$\dfrac{4}{5}A$$. **So, the correct answer is “Option C”.** **Note:** Since if all four resistances are arranged in such a way that ratio of resistance inside branches becomes equal then the circuit becomes balanced then current in diagonal branch becomes zero and this condition of circuit is called balanced condition and device is called as balanced wheatstone bridge.