Question

If ${{r}_{1}}$ and ${{r}_{2}}$ be the lengths of radii vectors of the parabola which are drawn at right angles to one another from the vertex, Prove that
${{r}_{1}}^{\dfrac{4}{3}}{{r}_{2}}^{\dfrac{4}{3}}=16{{a}^{2}}\left( {{r}_{1}}^{\dfrac{2}{3}}+{{r}_{2}}^{\dfrac{2}{3}} \right)$

Answer 1

Hint: The coordinates of points where radius vector touches parabola, say $P$ and $Q$, can be obtained as $\left( {{r}_{1}}\cos \theta ,{{r}_{1}}\sin \theta \right)$ and $\left( {{r}_{2}}\sin \theta ,-{{r}_{2}}\cos \theta \right)$. Then, these can be substituted in the equation of parabola to form equations.

Complete step by step answer:
Let us consider a parabola of the form ${{y}^{2}}=4ax$.
Since ${{r}_{1}}$ is a radius vector, let us consider that it makes an angle $\theta$ with the positive direction of $x-$axis and touches the parabola at point $P$.
So we can obtain the coordinates of point $P$ as $\left( {{r}_{1}}\cos \theta ,{{r}_{1}}\sin \theta \right)$.
Now, it is said in the question that ${{r}_{1}}$ and ${{r}_{2}}$ are drawn at right angles to one another from the vertex. So, we can conclude that ${{r}_{2}}$ makes an angle $90-\theta$ with the positive direction of the $x-$axis and touches the parabola at point $Q$.
So we can obtain the coordinates of point $Q$ as $\left( {{r}_{2}}\sin \theta ,-{{r}_{2}}\cos \theta \right)$.
Consider the figure as shown below.

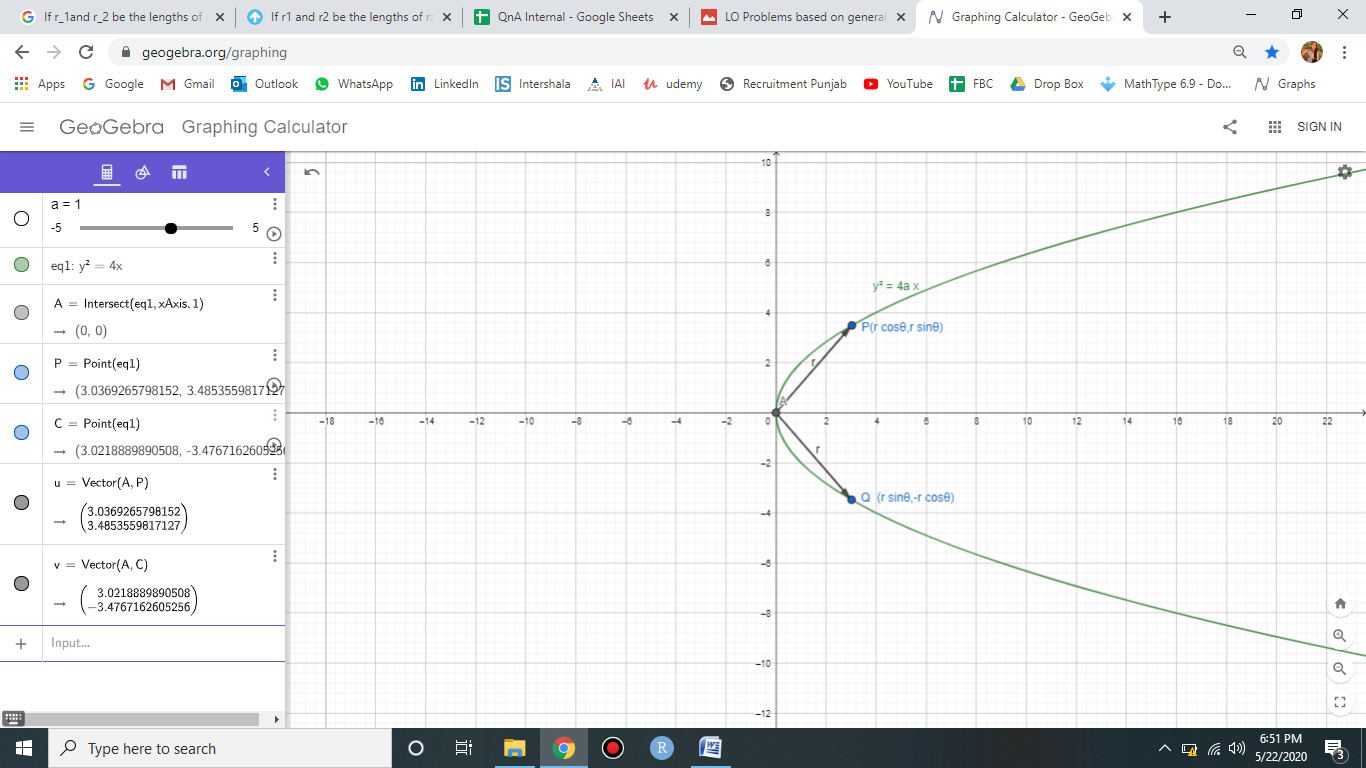
Now, since $P$ and $Q$ lie on the parabola, they satisfy the equation of the parabola.
Therefore, we can substitute $P$$$\left( {{r}{1}}\cos \theta ,{{r}{1}}\sin \theta \right)$in the parabola${{y}^{2}}=4ax$$ as shown below,

& {{\left( {{r}_{1}}\sin \theta \right)}^{2}}=4a{{r}_{1}}\cos \theta \\\ & {{r}_{1}}^{2}{{\sin }^{2}}\theta =4a{{r}_{1}}\cos \theta \\\ & {{r}_{1}}{{\sin }^{2}}\theta =4a\cos \theta \ldots \ldots \ldots \left( i \right) \\\ \end{aligned}$$ Now let us substitute the point $Q$$$\left( {{r}_{2}}\sin \theta ,-{{r}_{2}}\cos \theta \right)$$in the parabola $${{y}^{2}}=4ax$$ as shown below, $$\begin{aligned} & {{\left( -{{r}_{2}}\cos \theta \right)}^{2}}=4a{{r}_{2}}\sin \theta \\\ & {{r}_{2}}^{2}{{\cos }^{2}}\theta =4a{{r}_{2}}\sin \theta \\\ & {{r}_{2}}{{\cos }^{2}}\theta =4a\sin \theta \ldots \ldots \ldots \left( ii \right) \\\ \end{aligned}$$ Let us divide equation $$\left( i \right)$$ by $$\left( ii \right)$$ $\dfrac{{{r}_{1}}{{\sin }^{2}}\theta }{{{r}_{2}}{{\cos }^{2}}\theta }=\dfrac{4a\cos \theta }{4a\sin \theta }$ On cancelling the like terms, we get $\dfrac{{{r}_{1}}{{\sin }^{2}}\theta }{{{r}_{2}}{{\cos }^{2}}\theta }=\dfrac{\cos \theta }{\sin \theta }$ On rearranging the terms, we get $\dfrac{{{\sin }^{3}}\theta }{{{\cos }^{3}}\theta }=\dfrac{{{r}_{2}}}{{{r}_{1}}}$ Since we know that $\dfrac{\sin \theta }{\cos \theta }=\tan \theta $, we can write $\begin{aligned} & {{\tan }^{3}}\theta =\dfrac{{{r}_{2}}}{{{r}_{1}}} \\\ & \tan \theta ={{\left( \dfrac{{{r}_{2}}}{{{r}_{1}}} \right)}^{\dfrac{1}{3}}} \\\ \end{aligned}$ We can use the trigonometric relation $$\cos \theta =\dfrac{1}{\sqrt{1+{{\tan }^{2}}\theta }}$$ and substitute the above result in it. $$\begin{aligned} & \cos \theta =\dfrac{1}{\sqrt{1+{{\left[ {{\left( \dfrac{{{r}_{2}}}{{{r}_{1}}} \right)}^{\dfrac{1}{3}}} \right]}^{2}}}} \\\ & \cos \theta =\dfrac{1}{\sqrt{1+{{\left( \dfrac{{{r}_{2}}}{{{r}_{1}}} \right)}^{\dfrac{2}{3}}}}} \\\ \end{aligned}$$ Taking the LCM, we get $$\begin{aligned} & \cos \theta =\dfrac{1}{\sqrt{\dfrac{{{r}_{1}}^{\dfrac{2}{3}}+{{r}_{2}}^{\dfrac{2}{3}}}{{{r}_{1}}^{\dfrac{2}{3}}}}} \\\ & \cos \theta =\dfrac{\sqrt{{{r}_{1}}^{\dfrac{2}{3}}}}{\sqrt{{{r}_{1}}^{\dfrac{2}{3}}+{{r}_{2}}^{\dfrac{2}{3}}}} \\\ & \cos \theta =\dfrac{{{r}_{1}}^{\dfrac{1}{3}}}{\sqrt{{{r}_{1}}^{\dfrac{2}{3}}+{{r}_{2}}^{\dfrac{2}{3}}}} \\\ \end{aligned}$$ We can also use the trigonometric relation $$\sin \theta =\tan \theta \times \cos \theta $$ and substitute $\tan \theta ={{\left( \dfrac{{{r}_{2}}}{{{r}_{1}}} \right)}^{\dfrac{1}{3}}}$ and $$\cos \theta =\dfrac{{{r}_{1}}^{\dfrac{1}{3}}}{\sqrt{{{r}_{1}}^{\dfrac{2}{3}}+{{r}_{2}}^{\dfrac{2}{3}}}}$$ in it. So, we will get $\begin{aligned} & \sin \theta ={{\left( \dfrac{{{r}_{2}}}{{{r}_{1}}} \right)}^{\dfrac{1}{3}}}\times \dfrac{{{r}_{1}}^{\dfrac{1}{3}}}{\sqrt{{{r}_{1}}^{\dfrac{2}{3}}+{{r}_{2}}^{\dfrac{2}{3}}}} \\\ & \sin \theta =\dfrac{{{r}_{2}}^{\dfrac{1}{3}}}{{{r}_{1}}^{\dfrac{1}{3}}}\times \dfrac{{{r}_{1}}^{\dfrac{1}{3}}}{\sqrt{{{r}_{1}}^{\dfrac{2}{3}}+{{r}_{2}}^{\dfrac{2}{3}}}} \\\ & \sin \theta =\dfrac{{{r}_{2}}^{\dfrac{1}{3}}}{\sqrt{{{r}_{1}}^{\dfrac{2}{3}}+{{r}_{2}}^{\dfrac{2}{3}}}} \\\ \end{aligned}$ On substituting $$\cos \theta =\dfrac{{{r}_{1}}^{\dfrac{1}{3}}}{\sqrt{{{r}_{1}}^{\dfrac{2}{3}}+{{r}_{2}}^{\dfrac{2}{3}}}}$$ and $$\sin \theta =\dfrac{{{r}_{2}}^{\dfrac{1}{3}}}{\sqrt{{{r}_{1}}^{\dfrac{2}{3}}+{{r}_{2}}^{\dfrac{2}{3}}}}$$ in equation $$\left( i \right)$$, we get $$\begin{aligned} & {{r}_{1}}{{\left( \dfrac{{{r}_{2}}^{\dfrac{1}{3}}}{\sqrt{{{r}_{1}}^{\dfrac{2}{3}}+{{r}_{2}}^{\dfrac{2}{3}}}} \right)}^{2}}=4a\dfrac{{{r}_{1}}^{\dfrac{1}{3}}}{\sqrt{{{r}_{1}}^{\dfrac{2}{3}}+{{r}_{2}}^{\dfrac{2}{3}}}} \\\ & {{r}_{1}}\dfrac{{{r}_{2}}^{\dfrac{2}{3}}}{{{r}_{1}}^{\dfrac{2}{3}}+{{r}_{2}}^{\dfrac{2}{3}}}=4a\dfrac{{{r}_{1}}^{\dfrac{1}{3}}}{\sqrt{{{r}_{1}}^{\dfrac{2}{3}}+{{r}_{2}}^{\dfrac{2}{3}}}} \\\ \end{aligned}$$ On rearranging the terms, we get $$\begin{aligned} & {{r}_{1}}\dfrac{{{r}_{2}}^{\dfrac{2}{3}}}{{{r}_{1}}^{\dfrac{1}{3}}}=4a\dfrac{{{r}_{1}}^{\dfrac{2}{3}}+{{r}_{2}}^{\dfrac{2}{3}}}{\sqrt{{{r}_{1}}^{\dfrac{2}{3}}+{{r}_{2}}^{\dfrac{2}{3}}}} \\\ & {{r}_{1}}^{\left( 1-\dfrac{1}{3} \right)}{{r}_{2}}^{\dfrac{2}{3}}=4a\sqrt{{{r}_{1}}^{\dfrac{2}{3}}+{{r}_{2}}^{\dfrac{2}{3}}} \\\ & {{r}_{1}}^{\dfrac{2}{3}}{{r}_{2}}^{\dfrac{2}{3}}=4a\sqrt{{{r}_{1}}^{\dfrac{2}{3}}+{{r}_{2}}^{\dfrac{2}{3}}} \\\ \end{aligned}$$ Squaring both sides, we get $$\begin{aligned} & {{\left( {{r}_{1}}^{\dfrac{2}{3}}{{r}_{2}}^{\dfrac{2}{3}} \right)}^{2}}={{\left[ 4a\sqrt{{{r}_{1}}^{\dfrac{2}{3}}+{{r}_{2}}^{\dfrac{2}{3}}} \right]}^{2}} \\\ & {{r}_{1}}^{\dfrac{4}{3}}{{r}_{2}}^{\dfrac{4}{3}}=16{{a}^{2}}\left( {{r}_{1}}^{\dfrac{2}{3}}+{{r}_{2}}^{\dfrac{2}{3}} \right) \\\ \end{aligned}$$ Therefore, we have proved that if $${{r}_{1}}$$ and $${{r}_{2}}$$ be the lengths of radii vectors of the parabola which are drawn at right angles to one another from the vertex, $${{r}_{1}}^{\dfrac{4}{3}}{{r}_{2}}^{\dfrac{4}{3}}=16{{a}^{2}}\left( {{r}_{1}}^{\dfrac{2}{3}}+{{r}_{2}}^{\dfrac{2}{3}} \right)$$. Note: The choice of the parabola i.e. either $${{y}^{2}}=4ax$$ or $${{x}^{2}}=4ay$$ is important. Great attention must be paid as the points chosen will change accordingly. For the parabola, $${{x}^{2}}=4ay$$, the coordinates of points $P$ and $Q$ would be $$\left( {{r}_{1}}\cos \theta ,{{r}_{1}}\sin \theta \right)$$ and $$\left( -{{r}_{2}}\cos \theta ,{{r}_{2}}\sin \theta \right)$$ respectively.