Solveeit Logo
Login

Question

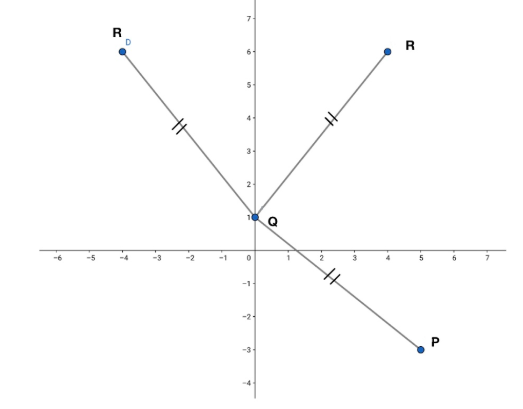
Question: If Q(0,1) is equidistant from P(5,-3) and R(x,6), find the values of x. Also find the distance QR an...

If Q(0,1) is equidistant from P(5,-3) and R(x,6), find the values of x. Also find the distance QR and PR.

Explanation

Solution

Hint: In this question it is given that the point Q(0,1) is equidistant from P(5,-3) and R(x,6), then we have to find the values of x. Also have to find QR and PR. So for this we have to know the distance formula between two points, which states that, the distance between the points A(a,b) to B(c,d) is d=(a−c)2+(b−d)2\mathbf{d} =\sqrt{\left( a-c\right)^{2} +\left( b-d\right)^{2} } ............(1)
Complete step-by-step solution:
Now by the above formula we can find the distance between Q(0,1) and P(5,-3),
QP=(0−5)2+(1−(−3))2=\sqrt{\left( 0-5\right)^{2} +\left( 1-\left( -3\right) \right)^{2} }
=(−5)2+(1+3)2=\sqrt{\left( -5\right)^{2} +\left( 1+3\right)^{2} }
=25+42=\sqrt{25+4^{2}}
=25+16=\sqrt{25+16}
=41=\sqrt{41}
And the distance between Q(0,1) and R(x,6),
QR=(0−x)2+(1−6)2=\sqrt{\left( 0-x\right)^{2} +\left( 1-6\right)^{2} }
=x2+(−5)2=\sqrt{x^{2}+\left( -5\right)^{2} }
=x2+25=\sqrt{x^{2}+25}
Now since, the distance between the QP and QR are equal, then we can write,
QP = QR
⇒41=x2+25\Rightarrow \sqrt{41} =\sqrt{x^{2}+25}
⇒x2+25=41\Rightarrow \sqrt{x^{2}+25} =\sqrt{41}
⇒(x2+25)=(41)2\Rightarrow \left( \sqrt{x^{2}+25} \right) =\left( \sqrt{41} \right)^{2} [squaring both side]
⇒x2+25=41\Rightarrow x^{2}+25=41
⇒x2=41−25\Rightarrow x^{2}=41-25
⇒x2=16\Rightarrow x^{2}=16
⇒x=±16\Rightarrow x=\pm \sqrt{16}
⇒x=±4\Rightarrow x=\pm 4
Therefore, the coordinate of R is either (4,6) or (-4,6)
Now, when R=(4,6)
QR=(0−4)2+(1−6)2\sqrt{\left( 0-4\right)^{2} +\left( 1-6\right)^{2} }
=16+25=41\sqrt{16+25} =\sqrt{41}
Similarly when R=(-4,6) then
QR=(0+4)2+(1−6)2\sqrt{\left( 0+4\right)^{2} +\left( 1-6\right)^{2} }
=16+25=41\sqrt{16+25} =\sqrt{41}

Now when R=(4,6)
PR=(5−4)2+(−3−6)2PR=\sqrt{\left( 5-4\right)^{2} +\left( -3-6\right)^{2} }
=1+(−9)2=1+81=82=\sqrt{1+\left( -9\right)^{2} } =\sqrt{1+81} =\sqrt{82}
And when R=(-4,6) then
PR=(5−(−4))2+(−3−6)2=92+92=\sqrt{\left( 5-\left( -4\right) \right)^{2} +\left( -3-6\right)^{2} } =\sqrt{9^{2}+9^{2}}
=81+81\sqrt{81+81}=162\sqrt{162}
Therefore we can say that the coordinate of R is (4,6) or (-4,6) and QR=41\sqrt{41} and PR=82\sqrt{82} or 162\sqrt{162} .
Note: While solving we got two coordinates for R, so why do we get two points? It is because in the first condition it is given that from point Q the distance of P and R are the same so there might be more than one point(point R) whose distance is equal to QP.
So you can understand it by a simple diagram,