Question

If PSQ is the focal chord of the parabola ${y^2} = 8x$ such that $SP = 6$. Then the length SQ is
A) $4$
B) $6$
C) $3$
D) None of these

Answer 1

In the given question we first compare the given equation of parabola ${y^2} = 8x$ with standard equation of parabola ${y^2} = 4ax$ .By comparing this we get the focal length of given parabola SQ. We know that the semi latus rectum of parabola is the harmonic mean between the segments of any focal chord. The harmonic mean formula is $\dfrac{2}{{\dfrac{{SP + SQ}}{{SP \times SQ}}}}$ By using this property we get the required answer.
A parabola is the locus of a point which moves in a plane such that its distance from a fixed point called focus is equal to its distance from a fixed straight line called directrix and focal chord is a chord that passes through the focus of a parabola.

Complete step by step solution:
We are given the parabola ${y^2} = 8x$such that $SP = 6$ then we have to find the length SQ.
We compare the above equation of parabola with the standard equation of parabola ${y^2} = 4ax$
On comparing this we get
$4a = 8$
$\Rightarrow a = \dfrac{8}{4}$
$\Rightarrow a = 2$
Therefore the focus of parabola $S\left( {2,0} \right)$

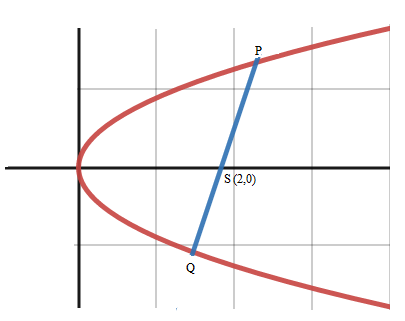
We know that latus rectum of parabola $= 4a$ $= 8$
Then semi latus rectum of parabola $= \dfrac{8}{2} = 4$
We know that the semi latus rectum of parabola is the harmonic mean between the segments SP and SQ of focal chord PQ. $\dfrac{2}{{\dfrac{{SP + SQ}}{{SP \times SQ}}}}$. We use the harmonic mean formula to find the length SQ.
$\because$ SP,$4$ and SQ are in H.P.
Semi latus rectum is harmonic mean of SP and SQ,
$4 = \dfrac{{2 \times SP \times SQ}}{{SP + SQ}}$
Since, Semi latus rectum is $4$
On putting the value of $SP = 6$, we get
$\Rightarrow 4 = \dfrac{{2 \times 6 \times SQ}}{{6 + SQ}}$
$\Rightarrow 4 \times \left( {6 + SQ} \right) = 12 \times SQ$
On multiplying $4$ inside the bracket
$\Rightarrow 24 + 4SQ = 12SQ$
On shifting $4SQ$ on right hand side
$\Rightarrow 24 = 12SQ - 4SQ$
$\Rightarrow 24 = 8SQ \\\ \Rightarrow SQ = \dfrac{{24}}{8} \\\ \Rightarrow SQ = 3 \\\$
Hence the required value of SQ is $3$.
Therefore option ‘c’ is correct.
As a result, If PSQ is the focal chord of the parabola ${y^2} = 8x$ such that $SP = 6$. Then the length SQ is $3$.

Note:
In this type of problem we should note that the half of the length of the latus rectum is the length of the semi latus rectum. And we should also remember the formula of harmonic mean. Because in this problem we use this formula for getting the required answer.