Question

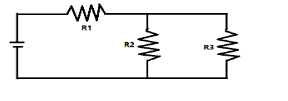
If power consumptions in $R_1$​, $R_2$​ & $R_3$​ are the same then what will be the relation between them?

A. ${R_1} = {R_2} = {R_3}$
B. ${R_2} = {R_3} = 2{R_1}$
C. ${R_2} = {R_3} = 4{R_1}$
D. ${R_1} = {R_2} = 4{R_3}$

Answer 1

As we all know that the power consumption in an electrical circuit is the product of the voltage and the current flowing in the circuit but power consumption in a circuit in the terms of the resistance will be $P = \dfrac{{{V^2}}}{R}$, and also $P = {I^2}R$. Hence from this relation we can conclude that the power consumption in a circuit is dependent on the voltage and the resistance and also on the current.

Complete answer:
Now on observing the given circuit we see that the resistors ${R_2}$ and ${R_3}$ are connected in parallel to each other and the combination of both of them is connected in series with the resistance ${R_1}$. Now if we assume that the current $I$ is flowing through the resistance ${R_1}$ and current ${I_1}$ is flowing through resistance ${R_2}$, then the current flowing through the resistance ${R_3}$ will be $I - {I_1}$.
Now applying current divider rule,
${I_1} = I \times \dfrac{{{R_3}}}{{{R_2} + {R_3}}}$-----equation (1)
It is given in the question that the power across all the resistors are the same, that is ${P_1} = {P_2} = {P_3}$.
Now if ${P_1} = {P_2}$,
Then ${I^2}{R_1} = {I_1}^2{R_2}$-------equation (2)
Also ${P_2} = {P_3}$
Voltage across ${R_2}$ and ${R_3}$will be the same.
$\Rightarrow \dfrac{{{V^2}}}{{{R_2}}} = \dfrac{{{V^2}}}{{{R_3}}}$
$\Rightarrow {R_2} = {R_3}$--------equation (3)
Now putting the values from equation (3) in equation (1), we get
${I_1} = I \times \dfrac{{{R_3}}}{{2{R_3}}}$
$\Rightarrow {I_1} = \dfrac{I}{2}$
Now putting the values in equation (2), we get
${I^2}R = {I_1}^2{R_2}$
$\Rightarrow {I^2}R = {\left[ {\dfrac{I}{2}} \right]^2}{R_2}$
$\Rightarrow {I^2}{R_1} = \dfrac{{{I^2}}}{4}{R_2}$
$\Rightarrow {R_1} = \dfrac{{{R_2}}}{4}$
$\Rightarrow 4{R_1} = {R_2}$----equation (4)
Now combining equation (3) and equation (4), we get
$\Rightarrow {R_2} = {R_3}and{R_2} = 4{R_1}$
$\Rightarrow {R_2} = {R_3} = 4{R_1}$

So, the correct answer is “Option C”.

Note:
The power consumption in the series combination is less than the parallel combination. For example, if we have to connect 12 LEDs of 25mA each across a 3V supply and we connect then in parallel then the consumed power will be 0.9 watts while if we connect the LEDs in the series connection then the power consumed will be 0.7watt. but the bulbs will glow brighter in the parallel connection while the bulbs in the series connections are dim. So finally, the parallel connection is better even though it consumes comparatively more power.