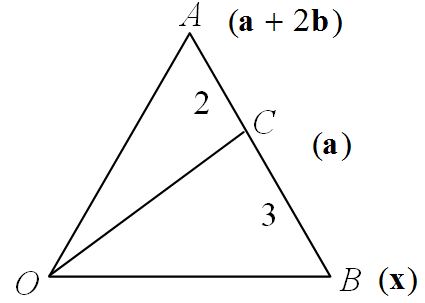Question

If position vector of a point Ais $\mathbf { a } + 2 \mathbf { b }$ and $\mathbf { a }$ divides AB in the ratio 2 : 3, then the position vector of B is

• A.
• B.
• C. $\mathbf { a } - 3 \mathbf { b }$
• D. $\mathbf { b }$

Answer 1

Answer: (C)

$\mathbf { a } - 3 \mathbf { b }$

Answer 2

Let position vector of B is .

The point $C ( \mathbf { a } )$ divides AB in 2 : 3.$\therefore$ $\mathbf { a } = \frac { 2 \mathbf { x } + 3 ( \mathbf { a } + 2 \mathbf { b } ) } { 2 + 3 }$

̃ $5 \mathbf { a } = 2 \mathbf { x } + 3 \mathbf { a } + 6 \mathbf { b }$

$\therefore$ $\mathbf { x } = \mathbf { a } - 3 \mathbf { b }$