Question

If point P(x, y) is called a lattice point, if $x,y\in I$. Then the total number of lattice points in the interior of the circle ${{x}^{2}}+{{y}^{2}}={{a}^{2}}$, $x\ne 0$ cannot be.
$\begin{aligned} & a)202 \\\ & b)203 \\\ & c)204 \\\ & d)205 \\\ \end{aligned}$

Answer 1

Now first we will try to plot the circle ${{x}^{2}}+{{y}^{2}}={{a}^{2}}$ . Now we know that this is a circle with center origin and radius a. Now we know that the circle is symmetric in each quadrant. Hence if there exist lattice points in one quadrant then the same number of lattice points exists in each quadrant. Also note that the origin also satisfies the lattice point definition. Hence the number of lattice points can be easily calculated.

Complete step by step solution:
Now consider the given circle ${{x}^{2}}+{{y}^{2}}={{a}^{2}}$ .
Now we know that this is a circle with centre as origin and radius a.
Hence we get the circle as,

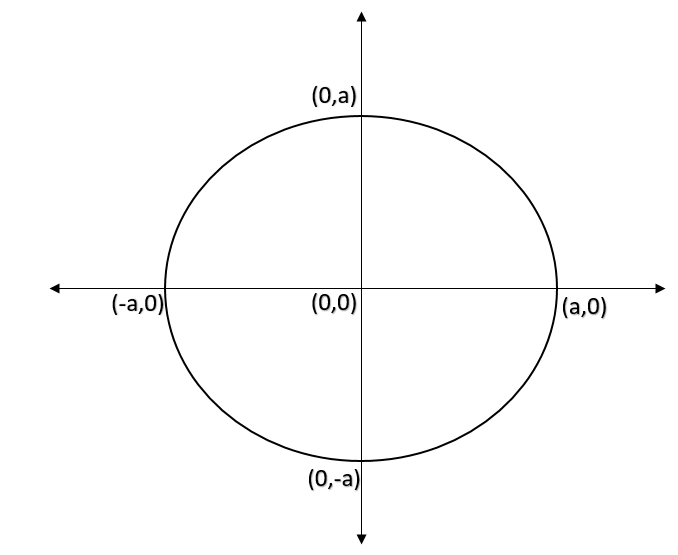
Now note that all the 4 quadrants share a similar area of circle.
Now we want to find lattice points of a circle. Lattice points are the points which are of the form $\left( x,y \right)$ where x and y both are integers.
Now let us say there are no lattice points in the first quadrant. Then since all the four quadrants are similar we can say that there will be no lattice point in each quadrant.
Hence we get a total of 4n lattice points in the four quadrants.
Now note that x and y can also be both zero since zero is an integer. Hence we have that the origin is also a lattice point.
Hence we get a total of $4n+1$ lattice points.
Now out of the given numbers only 205 is in the form $4n+1$.
Hence 202, 203, 204 cannot be the total number of lattice points.

So, the correct answer is “Option d)”.

Note: Now note that to check if the number is in the form of $4n+1$ we will check if the solution of the equation $4n+1=205$ gives value of n as an integer. Hence if we have $4n+1=204$ or other numbers we won’t get n as an integer.