Question
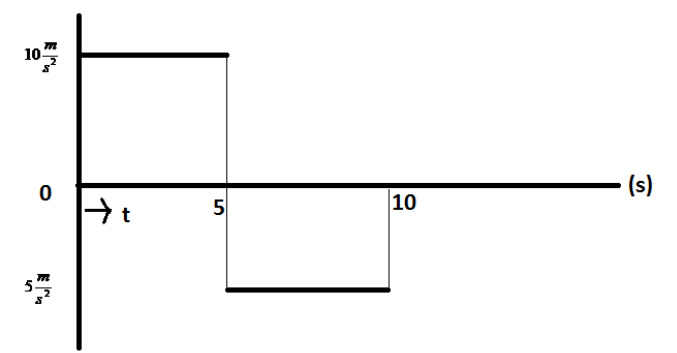
Question: If particle starts from \(10m/s\) then velocity of particle at \(t=10s\) according to given curve is...
If particle starts from 10m/s then velocity of particle at t=10s according to given curve is
Solution
To find the velocity at 10 seconds, we will use the first equation of linear motion for kinematics for constant acceleration. We will first find the velocity at 5 seconds for its particular acceleration and then using this velocity as initial velocity, we will find the final velocity of the object for a 5 to 10 seconds time period.
Complete step by step answer:
Here, we are given that the velocity of a particle when the time is zero is 10m/s and hence the particle’s initial velocity is 10m/s. We need to find the velocity of the particle at time t=10s. As in the curve it is given that the particle is moving at a constant acceleration for the first five seconds and the value of that acceleration is10s2m. For the next five seconds, the car is moving at a constant acceleration and the value of that acceleration is−5s2m. Now, to find the velocity at 10s, we will use the first equation of kinematics for constant acceleration twice; one for 5 seconds and the other for 5 to 10 seconds. Thus,
v=u+at
Where, v is the final velocity, u is the initial velocity, a is the constant acceleration and t is the time taken. Now, for the first five seconds,
v=10+(10)(5)=60sm
For the next five seconds;
